Salut à tous,

Je viens solliciter votre aide car je suis actuellement bloqué sur un exercice.

Voici l'énoncé :
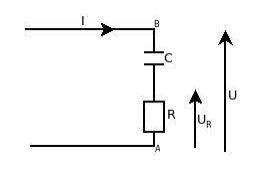
On considère le montage en série suivant composé d'une résistance R et d'un condensateur de capacité C. (Voir image attaché)

L'amplitude de l'intensité I est I.
L'amplitude de la tension U entre A et B est U = (R+)I et celle aux bornes de la résistance est U_r=RI.

On définit la fonction de transfert donc ou encore (résultat admis).

On pose et , on a alors

1. Cas particulier : u=1 c'est à dire =₀

a) Déterminer la forme algébrique de T(j).
b) Calculer le module et un argument de T(j).
c) En déduire la forme trigonométrique et la forme exponentielle de T(j).

J'ai pu répondre à ces trois premières questions sans trop de difficulté, avec u qui vaut 1, j'ai pas eu de soucis.

Par contre dans le cas général, je ne sais pas trop comment m'y prendre :

2. Cas général :

a) Ecrire la forme algébrique de T(j) en fonction de u.
Pour répondre à cette question, j'ai essayé de m'y prendre comme pour le a de la première partie :


Et à partir de là, je n'arrive plus à avancer, je n'arrive pas à retrouver de forme du type a+ib.

Désolé pour le pavé, j'espère qu'une âme charitable voudra bien m'aider, à très bientôt !