Inscription / Connexion Nouveau Sujet
optimisation dans l'espace
Bonjour à tous,
l'énoncé du sujet qui me pose problème est à cette adresse : ** lien vers l'énoncé effacé **
la figure donne ca: 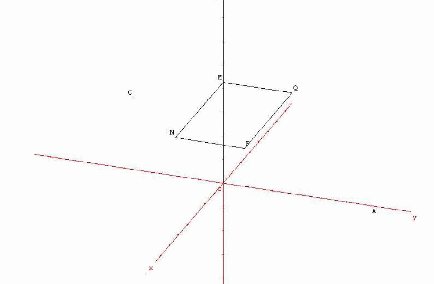
L'aire de MNPQ est donc maximale quand M milieu de [OB] c'est à dire quand M(0;4)
Mais je n'arrive à pas à trouver la manière d'exprimer MN et MQ en fonction de z... c'est à dire la question 3
il faut utiliser les vecteurs, coordonnées.. ?
merci
Edit Coll : si tu veux de l'aide, merci de faire l'effort de recopier ton énoncé sur le forum 
![]() [lien]
[lien]
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]() [lien]
[lien]
Bonjour
Une des règles de ce forum est de recopier l'énoncé (le scan des figures est en revanche accepté)

Dans un repère orthonormal, on considere les points A(0 6 0) B(0 0 8) et C(10 0 8)
M est un point appartenant au segment [OB]
Le plan P passe par M et est orthogonal à (OB) et coupe la droite (AC) en P
On note N et Q les points d'intersections du plan P avec les droites (OC) et (AB)
On cherche à trouver la position de M pour que l'aire du rectangle MNPQ soit maximale
Questions:
On note Z=OM
1) exprimer en fonction de z les longueurs MN et MQ
2) Vérifier la conjecture ( c'est à dire, que l'aire est maximale quand M est au milieu de [ob] quand M(0 4)
voila lol


