Inscription / Connexion Nouveau Sujet
Orthogonalité dans un cube
Bonsoir à tous,
Actuellement, en train de réviser la géométrie dans l'espace, je bloque sur une affirmation :
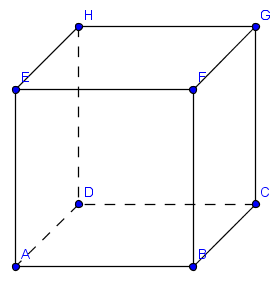
Dans le plan ABCDEFGH (voir image jointe),
- il est affirmé que (FC) est orthogonale à (GB) et (HG), donc orthogonale au plan (HGB), et par conséquent orthogonale à la droite (HB) de ce plan.
Je suis d'accord sur le fait que (FC) est orthogonale à (GB) car diagonale d'un carré. Mais pourquoi donc (FC) est-elle orthogonale à HG ? Je ne vois pas du tout.
Quelqu'un pourrait-il m'expliquer ?
Un grand merci d'avance pour la lumière que vous m'apportez !
Salut,
pourquoi donc (FC) est-elle orthogonale à HG ?
Milles mercis Yzz pour ton aide !
Je viens d'enchaîner 5 heures de mathématiques, et je pense que je fatigue si de telle évidence m'échappe.
L'exercice se poursuit par une autre affirmation :
(HB) est orthogonale aux deux droites sécantes (FA) et (FC) du plan (FAC) donc orthogonale à ce plan.
Si j'ai bien compris : (HB) est orthogonale à (BF) et (BA) donc orthogonale à (BAF), c'est à dire au plan (BAF) d'où HB est orthogonale à (FA). De plus, (HB) est orthogonale à (FB) et (BC) donc orthogonale à (FBC), c'est à dire à (FC).
Peux-tu me confirmer ma justification ?
Merci d'avance.
Mince, je comprends maintenant pourquoi (HB) n'est pas orthogonale à (BF).
Mais, comment alors peut-on justifier que (HB) est orthogonale à (FA) et à (FC) ?
Dans le premier cas, on est obligé de faire intervenir le plan (FAC) contenant la droite (FA), d'où mon idée pour (BF).
Merci pour ta réponse Yzz !
C'est très appréciable d'avoir des personnes comme toi sur le forum.
Bonne soirée.
Avant de te laisser, pour montrer que (HB) est orthogonale à (FC), voici ma réponse :
(FC) est orthogonale à (GB) et (HA) donc au plan (GBHA), donc à (HB).
Qu'en penses-tu ?
Merci.
Parfait  !
!
Bonne soirée et merci encore une fois pour tes explications simples mais pédagogiques et simples !
Le topic peut être clos.



