Bonsoir,

Oui... mais il faut quand même se mettre dans un triangle !

Ça n'est pas non plus extrêmement dur : il suffit de tracer une diagonale de ton parallélogramme et hop, tu as deux triangles. Il suffit ensuite de faire tes calculs pour montrer que ton parallélogramme est rectangle (d'après la réciproque de Pythagore)

Le plus dur est de trouver la mesure de la diagonale, vue que tu ne peux naturellement pas utiliser Pythagore dans un des triangles de ton parallélogramme (pour cela, il faudrait savoir que ton triangle est rectangle... autrement dit tu sais déjà que ton parallélogramme est un rectangle).



PS : Généralement, pour montrer qu'un parallélogramme est un rectangle, on travaille plutôt sur les propriétés des diagonales : « un rectangle est un parallélogramme dont les diagonales se coupent en un même milieu ».

Merci de me répondre. Je vais essayer de faire l'exercice en question...
Je pensais effectivement qu'en coupant mon parallelogramme en 2 par une diagonale, j'allais avoir 2 triangles et je comptais utiliser Pythagore pour les deux.....

... la réciproque : le théorème de Pythagore, tu ne peux l'appliquer que si tu sais que ton triangle est rectangle*. Or, c'est ce que tu veux montrer ici...

Autre petite chose : ça ne sert à rien de le faire pour les deux. Il suffit de montrer que tu as un angle droit, et tu peux en déduire que ton parallélogramme est rectangle. Je te laisse comprendre pourquoi, ça se démontre assez (très) facilement avec la propriété « si deux droites sont perpendiculaires, toute parallèle à l'une est perpendiculaire à l'autre » (bon, en fait, la démo est faite ).

Mais enfin, cette méthode peut très bien marcher ici si tu as un moyen de calculer la mesure de la diagonale (ou si tu la connais déjà...), tout dépend de ton énoncé !



* on l'utilise aussi pour justifier qu'un triangle n'est pas rectangle, enfin c'est des notions de logique qui sont un peu difficile en 4e.

En fait, voici mon enoncé :

Construire un parallélogramme RSTU tel que :

RS = 7,2 cm  ST = 3,5 cm  et US = 8 cm

Le parallélogramme RSTU est il un rectangle ? Justifier la réponse

J'ai tracé la figure sur papier mais j'hésite beaucoup.

Je peux dire que RS // UT et que RU // ST

Je n'arrive pas à avancer plus...

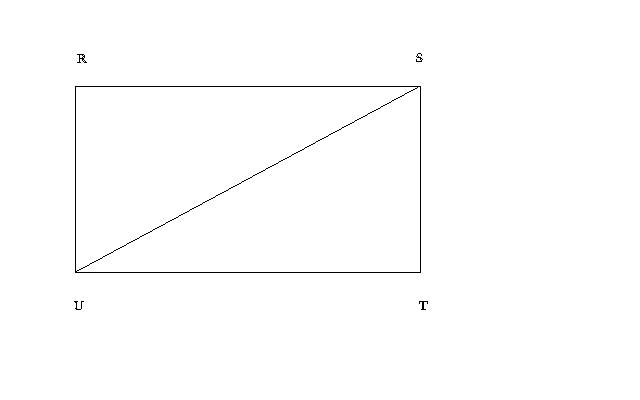
Ah bah voilà, alors je peux te dire que c'est bien par la réciproque de Pythagore qu'il faut passer.

Tout d'abord, on peut dire que RU=ST=3,5cm car dans un parallélogramme, les côtés opposés ont même longueur. Dans le triangle RSU, on a donc :
> RS = 7,2cm
> RU = 3,5cm
> US = 8cm

On a donc RU<RS<US, tu peux donc dire que seul le côté [...] peut être l'hypoténuse.

Autrement dit, il suffit de calculer séparément :
..² = ...
..² + ..² = ...

Et de voir si ces deux calculs sont égaux (ou pas ).

Pardon, c'est bien « par Pythagore » qu'on va passer : réciproque ou pas, à toi de voir (cf. le * à la fin de mon message de 20:41).

Merci beaucoup pour votre aide.


Alors SU est l'hypothenuse de RSU.
Je compare SU² et RS² et RU²

SU² = 8² = 64
RS² + RU² = 7,2² + 3,5² = 51,84 + 12,25 = 64
Donc SU² = RS² + RU²
On peut donc dire d'après le théoreme de Pythagore que le triangle RSU est un triangle rectangle en R.

On sait que RSTU est un parallélogramme et S^RU = 90° or si un parallélogramme a un angle droit alors c'est un rectangle . Donc RSTU est un rectangle

????? Merci pour votre correction

Attention, quand tu conclus :
> si tu conclus que ton triangle est rectangle, c'est d'après la réciproque du théorème de Pythagore ;
> si tu conclus que ton triangle n'est pas rectangle, c'est d'après le théorème de Pythagore.

Mais au fait, 51,84+12,25, ça fait vraiment 64 ?

OK donc c'est toujours ainsi ?
Pour démontrer qu'un triangle n'est pas rectangle c le théorème de Pythagore et pour démontrer qu'il est rectangle c la réciproque du théoreme ?? Je m'embrouille avec çà.

51,84 + 12,25 = 64,09 cm mais je me suis dit qu'il fallait arrondir... puisque çà m'arrangeait. En plus c la question que je voulais poser. Peux tu m'expliquer STP ?

Et vraiment un grand merci

Pour la première question, en gros oui. On ne peut pas vraiment dire qu'on « utilise » le théorème ou sa réciproque, parce qu'on ne sait pas lequel on va utiliser pendant qu'on fait les calculs.

En fait, pour chaque théorème on a :
> le théorème en lui-même : ici, « si ABC rectangle en A, alors AB²+AC²=BC² » ;
> la réciproque du théorème (qui n'est pas toujours vraie, tout dépend du théorème) : ici « si AB²+AC²=BC², alors ABC rectangle en A » ;
> la contraposée du théorème (qui est TOUJOURS vraie si le théorème est vrai) : ici, « si on n'a pas AB²+AC²=BC², alors ABC n'est pas rectangle en A ».

Quand ton triangle est rectangle, tu peux donc conclure d'après la réciproque du théorème, tandis que quand il ne l'est pas tu peux conclure d'après la contraposée du théorème. Et vu que cette contraposée découle directement du théorème, on dis « d'après le théorème de Pythagore »...

Bref, si tu comprends, tant mieux ; si tu ne comprends pas, ça n'est pas bien grave !

--
Sinon, pour répondre à ton autre question, tu ne dois pas arrondir ! Tu auras d'ailleurs remarqué que la question n'est pas « Démontrer que RSTU est un rectangle » mais « Le parallélogramme RSTU est il un rectangle ? »...

Oui mais si je n'arrondis pas
SU² ne sera pas egal a RS² + RU² et le triangle ne sera pas rectangle ????
Excuse mais je suis pas une fortiche des maths !

SVP quelqu'un peut il répondre à ma dernière question ??
et me dire si finalement le parallélogramme est un rectangle ?
Merci

Oui, mais c'est justement l'intérêt de l'exercice : si tu traces ta figure, tu dois avoir l'impression que ton parallélogramme est un rectangle. Mais lorsque tu fais tes calculs, tu te rends compte que ça n'est pas le cas...

En fait, plus la différence (RS²+RU²)-US² est petite, plus ton parallélogramme semble être un rectangle. Ici, cette différence ne vaut que 0,09, d'où la différence observations/théorie.



PS : Et je le répète, dans ton énoncé, on ne t'a jamais dit que ton parallélogramme devait être un rectangle. Il ne faut pas être déstabilisé par le fait que tu trouves que ça n'est pas un rectangle...

Merci infiniment Porcepic
Je comprends bien et effectivement çà change tout.
Sincèrement un grand merci pour toutes tes explications

Je t'en prie, c'était avec grand plaisir.