Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Fonction LogarithmeTopics traitant de Fonction Logarithme [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

paramètre et fonction ln

Posté par
Cornelia 14-12-12 à 13:13

salut,
soit fm(x)=xln|x|-(x-m)ln|x-m| (m*) x0 et xm
fm(0)=fm(m)=mln|m|

supposons que m>o et I=[m/2;+[
1 etudier la continuité t la dérivabilité de fmen 0 et en m
2 calculer la dérivée de fm et donner son tableau de variation
3 etudier la branches infinies de la fonction en+
voilà.; .c'est surtout dans la dérivabilité en 0 et m que je trouve des problème...j'ai bien utilisé des moyens..mais les limites à calculer  restent sous une forme indéfinie..un p'tit aide? j'en serais très reconaissante et merci d'avance

Posté par
cailloux Correcteurre : paramètre et fonction ln 14-12-12 à 14:47

Bonjour,

Par exemple en 0 (où f est continue) avec m>0:

\dfrac{f(x)-f(0)}{x}=\dfrac{x\ln|x|-(x-m)\,\ln|x-m|-m\,\ln\,m}{x}

\dfrac{f(x)-f(0)}{x}=\ln\left|\dfrac{x}{x-m}\right|+\dfrac{m}{x}\,\ln\left|\dfrac{x-m}{m}\right|

\dfrac{f(x)-f(0)}{x}=-\ln\left|1-\dfrac{m}{x}\right|+\dfrac{x}{m}\,\ln\left|\dfrac{x}{m}-1\right|

\dfrac{f(x)-f(0)}{x}=-\ln\left|1-\dfrac{m}{x}\right|-\dfrac{\ln\,\left|1-\frac{x}{m}\right|}{-\frac{x}{m}}

et avec \lim\limits_{h\to 0}\dfrac{\ln\,(1+h)}{h}=1, on obtient:

\lim\limits_{x_to 0}\dfrac{f(x)-f(0)}{x}=-\infty

f n' est pas dérivable en 0 (mais tangente verticale en A(0;m\,\ln\,m)

Posté par
cailloux Correcteurre : paramètre et fonction ln 14-12-12 à 14:51

Pour la dérivabilité en m, il suffit de remarquer (et de prouver) que la courbe présente un axe de symétrie d' équation x=\dfrac{m}{2}.

f ne sera pas non plus dérivable en m ...



Posté par
cailloux Correcteurre : paramètre et fonction ln 14-12-12 à 15:12

Une faute de frappe à la 3ème ligne de calcul qui ne change rien pour la suite:

\dfrac{f(x)-f(0)}{x}=-\ln\left|1-\dfrac{m}{x}\right|+\dfrac{m}{x}\,\ln\left|\dfrac{x}{m}-1\right|

Posté par
Corneliare : paramètre et fonction ln 14-12-12 à 18:08

oui..on nous a déjà dit de démontrer que x=m/2 et un axe de symétrie de la courbe..mais comment dire pour exploiter ceci?

Posté par
cailloux Correcteurre : paramètre et fonction ln 14-12-12 à 18:58

Mais si la droite d' équation x=\dfrac{m}{2} est axe de symétrie de la courbe, comme le point A(0;m\, \ln\,m) appartient à cette courbe avec une tangente verticale en ce point, alors le symétrique par rapport à cet axe soit B(m;m\,\ln\,m) appartient aussi à la courbe et la tangente en B d' abscisse m sera verticale itou.

Bref, en m, f n' est pas dérivable.

Un dessin:

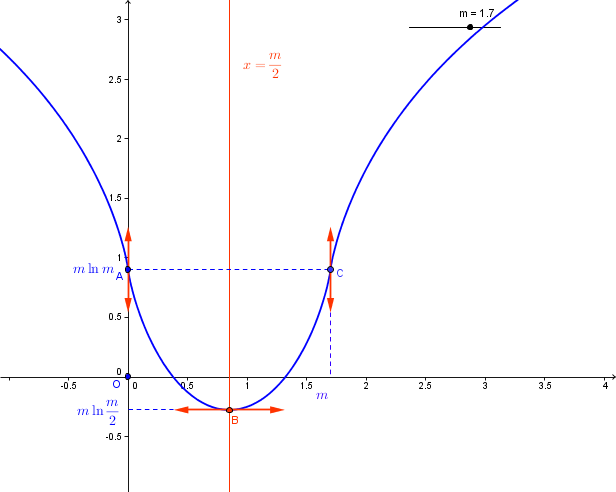
paramètre et fonction ln

A l' oeil, il semblerait que les deux tangentes en A et C ne sont pas verticales et pourtant elles le sont!

Posté par
Corneliare : paramètre et fonction ln 14-12-12 à 20:27

merci

Posté par
cailloux Correcteurre : paramètre et fonction ln 14-12-12 à 21:09

Posté par
Corneliare : paramètre et fonction ln 15-12-12 à 15:23

A propos des branches infinies de la courbe??

Posté par
Corneliafm(x)=xln|x|-(x-m)ln|x-m| 15-12-12 à 15:37

salut,
fm(x)=xln|x|-(x-m)ln|x-m| x0 et xm    m*
fm(0)=fm(m)=mln|m|
1 montrer que la courbe C-m=SO(Cm) où SO et la symétrie centrale du centre O
2 montrer que si m>2 alors fm ne s'annule pas
3 donner le nombre de zéro de f2
4 montrer que si 0<m<2 alors fm s'annule ne 2 points m<m avec m+m=m
5 dans cette partie, on suppose que 0<m<1
a montrer que m<m <1
b montrer que f1(m/m=-lnm
bon... ce n'est pas l'exercice complet.mais..voià..je ne comprends pas ce qui est demandé dans la 1 question et pour la suite... je n'ai aucune idée comment commencer..alors un petit aide..j'en serais vraiment très très reconnaissante et merci d'avance

*** message déplacé ***
* Océane > pose toutes les questions de ton exercice dans le même topic Cornelia, merci *

Posté par
cailloux Correcteurre : paramètre et fonction ln 15-12-12 à 17:57

Il suffit de regarder en +\infty. Par symétrie, on aura l' autre branche:

\lim\limits_{x\to +\infty}\dfrac{f(x)}{x}=\lim\limits_{x\to +\infty}\left(\ln\left|\dfrac{x}{x-m}\right|+m\,\dfrac{\ln\,|x-m|}{x}\right)=0

Donc branche parabolique d' axe (Ox) en +\infty

Même chose en -\infty

Posté par
Labore : fm(x)=xln|x|-(x-m)ln|x-m| 15-12-12 à 18:39

Bonsoir,
1) on te demande de montrer que les courbes représentant les fonctions  pour m et -m
fm(x)=xln|x|-(x-m)ln|x-m|
et f(-m)(x)=xln|x|-(x-(-m))ln|x-(-m)|
sont symétriques par rapport au point 0
autrement dit :
montre que pour tout x de Df
-x apparient  à Df et
fm(x)=-f(-m)(-x)


*** message déplacé ***

Posté par
cailloux Correcteurre : fm(x)=xln|x|-(x-m)ln|x-m| 15-12-12 à 18:54

Bonjour Labo,

Multiplet ou pas? paramètre et fonction ln

Je dis oui...



*** message déplacé ***

Posté par
cailloux Correcteurre : fm(x)=xln|x|-(x-m)ln|x-m| 15-12-12 à 18:54

Euh multipost!

*** message déplacé ***

Posté par
Labore : fm(x)=xln|x|-(x-m)ln|x-m| 15-12-12 à 19:08

Bonsoir Cailloux
Je pense comme toi

multipost


*** message déplacé ***

Posté par
Corneliare : fm(x)=xln|x|-(x-m)ln|x-m| 15-12-12 à 22:14

c'est la même fonction, je l'admet.. mais pas les mêmes questions... car je pensais que je pouvais faire le reste seule..mais voilà que je me bloques..c'est tout!

*** message déplacé ***

Posté par
cailloux Correcteurre : fm(x)=xln|x|-(x-m)ln|x-m| 15-12-12 à 22:21

Si à chaque question d' un exercice on devait ouvrir un nouveau topic ...

*** message déplacé ***

Posté par
Corneliare : paramètre et fonction ln 15-12-12 à 22:22

deux petites dernières choses... je sais que je vous ai un peu dérangé..mais..
1 pourriez-vous me reformuler ce que vous avez dit à propos de la non-dérivabilité en m..car je ne pense pas que j'ai bien saisi et
2   (Lien cassé)
et merci encore une fois et désolée pour le dérangement..

Posté par
cailloux Correcteurre : paramètre et fonction ln 16-12-12 à 15:47

Regarde le dessin:

A et C sont deux points de la courbe symétriques par rapport à la droite d' équation y=\dfrac{m}{2}, d' abscisses respectives 0 et m

On sait que la tangente à la courbe en A est verticale.

Donc par symétrie, la tangente en C, d' abscisse m, à la courbe sera verticale aussi.

Autrement dit f n' est pas dérivable en m

Posté par
Corneliare : paramètre et fonction ln 16-12-12 à 17:51

okay..désolée pour le muripost.;je ne l'ai pas fait exprès...mais pourriez-vous m'aider à propos de la deuxième partie où il ya ces et s'il vous plait??

Posté par
Corneliare : paramètre et fonction ln 16-12-12 à 17:53

multipost*

Posté par
cailloux Correcteurre : paramètre et fonction ln 17-12-12 à 00:20

4)Si 0<m<2, et 0<\dfrac{m}{2}<1 si bien que le minimum de f_m soit m\,\ln\,\dfrac{m}{2} est négatif.

Il reste à utiliser le TVI dans le cas des fonctions monotones sur les intervalles ]-\infty;\dfrac{m}{2}] et [\dfrac{m}{2};+\infty[ pour prouver l' existence de \alpha_m et \beta_m

De plus ces deux valeurs étant symétriques par rapport à \dfrac{m}{2}, on a \alpha_m+\beta_m=m (regarde la figure)

5)a) 0<m<1

f_m(m)=m\,\ln\,m<0 et f_m(1)=(m-1)\,\ln\,(1-m)>0

donc avec la croissance stricte de f_m sur [\dfrac{m}{2};+\infty[:

m<\beta_m<1

Posté par
cailloux Correcteurre : paramètre et fonction ln 17-12-12 à 13:56

5)b) Avec 0<m<\beta_m<1 d' où \beta_m-m>0 et \dfrac{\beta_m}{m}-1>0:

f_1\left(\dfrac{\beta_m}{m}\right)=\dfrac{\beta_m}{m}\,\ln\,\left(\dfrac{\beta_m}{m}\right)-\left(\dfrac{\beta_m}{m}-1\right)\,\ln\,\left(\dfrac{\beta_m}{m}-1\right)

f_1\left(\dfrac{\beta_m}{m}\right)=\dfrac{1}{m}\left[\underbrace{\beta_m\,\ln\,\beta_m-(\beta_m-m)\,\ln\,(\beta_m-m)}_{f_m(\beta_m)=0}-\beta_m\,\ln\,m+(\beta_m-m)\,\ln\,m\right]

f_1\left(\dfrac{\beta_m}{m}\right)=-\ln\,m


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !