Partie entière, exercice de trigonométrie

 Niveau Prepa (autre)Partager :
			        
Partie entière
Posté par 
KiyotakaMath  06-04-22 à 18:00
Bonjour,

on définit  la partie entière de la façon suivante : xE(x)

l'idée c'est de montrer que la suite (E(e2n)) pour n dans * est croissante. Moi j'aurai dit dans un premier temps que la suite (e2n)est croissante et que la suite (E(n)) est croissante, par composition la suite (E(e2n)) l'est.

Mais j'ai eu droit à une autre justification qui est la suivante, on regarde la différence de deux termes consécutifs pour voir si la différence est supérieure à 0 mais on a mieux que ça encore.

La justification est la suivante :

n*:E(e2(n+1))-E(e2n)1 car n*: e2(n+1)-e2ne2(e2-1)1.

Quelqu'un pourrait-il m'expliquer pourquoi cette assertion est-elle vraie ?
 Posté par 
lafol re : Partie entière  06-04-22 à 18:27
bonjour

laquelle ?
 Posté par 
KiyotakaMathre : Partie entière  06-04-22 à 18:30
bonjour, 

j'aimerai qu'on m'explique la justification qui m'a été donnée, c'est à dire la dernière assertion écrite ci-dessus :

merci

 Posté par 
Rintarore : Partie entière  06-04-22 à 18:43
Bonjour,

pour tout réel x et pour tout entier naturel n, on a E(x+n) = E(x) + n. Ici ça peut aider. 
 Posté par 
carpediemre : Partie entière  06-04-22 à 18:47
salut

et ton argument de croissance est valable ...

mais on peut se demander si la suite n'est pas constante ...

l'argument qu'on te donne prouve que la suite est strictement croissante ...
 Posté par 
KiyotakaMathre : Partie entière  06-04-22 à 18:52
ce que vous dites Rintaro est vrai mais je ne vois pas où vous voulez en venir...
 Posté par 
KiyotakaMathre : Partie entière  06-04-22 à 18:55
tout à fait carpediem, mais justement je ne comprends pas pourquoi le fait que :

 Posté par 
KiyotakaMathre : Partie entière  06-04-22 à 18:59
tout à fait carpediem, mais justement je ne comprends pas pourquoi le fait que :

 Posté par 
liona24re : Partie entière  06-04-22 à 19:00
On a  e2(n+1)-e2n=e2n(e2-1)

et je crois que la suite est claire
 Posté par 
KiyotakaMathre : Partie entière  06-04-22 à 19:02
Bon j'ai eu un soucis au niveau des réponses,

en clair je ne comprends pas pourquoi le fait que la différence de termes consécutifs de la suite (e^2n) est supérieure à 1 (je comprends bien pourquoi cela est vraie), justifie le fait que la différence de deux consécutifs de la suite (E(e^2n)) est elle-même supérieure ou égale à 1.
 Posté par 
KiyotakaMathre : Partie entière  06-04-22 à 19:03
liona24 @ 06-04-2022 à 19:00

On a  e2(n+1)-e2n=e2n(e2-1)

et je crois que la suite est claire

Justement, c'est la suite qui n'est pas claire pour moi
 Posté par 
carpediemre : Partie entière  06-04-22 à 19:08
il est clair que si y > x + 1 alors E(y)  E(x) + 1

d'après la propriété rappelée par Rintaro ...
 Posté par 
KiyotakaMathre : Partie entière  06-04-22 à 19:19
carpediem @ 06-04-2022 à 19:08

il est clair que si y > x + 1 alors E(y)  E(x) + 1

d'après la propriété rappelée par Rintaro ...

Bah oui c'est évidement... je ne sais pas pourquoi je n'ai pas voulu composer avec l'application partie entière...

Merci beaucoup à vous carpediem, liona24 et Rintaro
  Posté par 
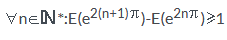
carpediemre : Partie entière  06-04-22 à 20:10
de rien