Niveau quatrième

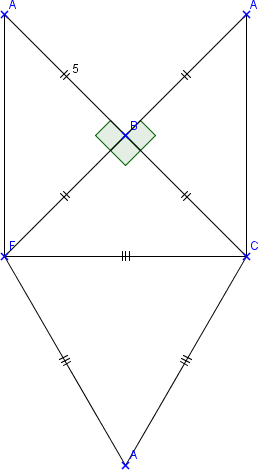
Patron d'un tétraèdre trirectangle

Posté par
Zakk 14-05-11 à 00:08

Bonsoir, j'ai un gros blocage sur un simple exercice.
Je ne me souviens plus comment faire un patron de tétraèdre trirectangle.
La figure s'appelle ACFB et est tétraèdre trirectangle en B.
On sait que AB=BF=BC=5cm
On sait aussi que AC=CF=AF puisque la pyramide est dans un cube.
Voilà, j'espere que vous me comprenez.

Merci d'avance.

Posté par re : Patron d'un tétraèdre trirectangle 14-05-11 à 01:16

J'ai jamais bossé sur ce type de pyramide mais d'instinct, je dirais que ça doit ressembler à ça :

$Patron d\'un tétraèdre trirectangle$

Posté par re : Patron d'un tétraèdre trirectangle 14-05-11 à 11:57

Ok merci beaucoup
Et l'aire des triangles rectangles est bien égale à 12,5 cm ?
Et par contre j'arrive pas à trouver celle exact du triangle équilatéral (FCA)...

Posté par re : Patron d'un tétraèdre trirectangle 14-05-11 à 13:37

Oui l'aire des triangles rectangles est bien 12,5cm² (n'oublie pas le carré)

Pour le triangle équilatéral, il faut faire (base x hauteur)/2 comme pour un triangle quelconque...

Calculons la base (c'est-à-dire FC)
Sachant que FBC est un triangle rectangle, le théorème de Pythagore s'applique :

$FC^2=BC^2+BF^2 \\ FC^2=5^2+5^2 \\ FC^2=25+25 \\ FC^2=50 \\ FC=\sqrt{50} \\ FC=\sqrt{25\times2} \\ FC=5\sqrt{2}cm$

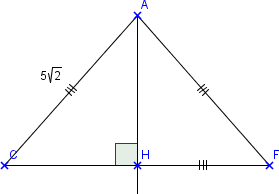
Calculons la hauteur
Donc appelons H le pied de la hauteur du triangle AFC issue de A (voir figure en bas).

$CH=\frac{CF}{2} \\ CH=\frac{5\sqrt{2}}{2}cm$

AHC est un triangle rectangle donc le théorème de Pythagore s'applique :

$AC^2=HA^2+CH^2 \\ (5\sqrt{2})^2=HA^2+(\frac{5\sqrt{2}}{2})^2 \\ 25\times2=HA^2+\frac{(5\sqrt{2})^2}{2^2} \\ 50=HA^2+\frac{25\times2}{4} \\ 50=HA^2+\frac{50}{4} \\ 50=HA^2+\frac{25}{2} \\ HA^2=50-\frac{25}{2} \\ HA^2=\frac{100}{2}-\frac{25}{2} \\ HA^2=\frac{75}{2} \\ HA=\sqrt{\frac{75}{2}} \\ HA=\frac{\sqrt{75}}{\sqrt{2}} \\ HA=\frac{\sqrt{25\times3}}{\sqrt{2}} \\ HA=\frac{5\sqrt{3}}{\sqrt{2}} \\ HA=\frac{5\sqrt{3}\times\sqrt{2}}{\sqrt{2}\times\sqrt{2}} \\ HA=\frac{5\sqrt{6}}{2}cm$

Calcul de l'aire
Maintenant qu'on connait la base et la hauteur, on peut calculer l'aire :

$A=\frac{base\times hauteur}{2} \\ A=\frac{CF\times AH}{2} \\ A=\frac{5\sqrt{2}\times\frac{5\sqrt{6}}{2}}{2} \\ A=\frac{\frac{5\sqrt{6}\times5\sqrt{2}}{2}}{2} \\ A=\frac{\frac{25\sqrt{12}}{2}}{2} \\ A=\frac{\frac{\sqrt{625\times12}}{2}}{2} \\ A=\frac{\frac{\sqrt{7500}}{2}}{2} \\ A=\frac{\frac{\sqrt{2500\times3}}{2}}{2} \\ A=\frac{\frac{50\sqrt{3}}{2}}{2} \\ \fbox{A=\frac{25\sqrt{3}}{2}cm^2}$

Des questions ?

$Patron d\'un tétraèdre trirectangle$

Posté par re : Patron d'un tétraèdre trirectangle 14-05-11 à 17:17

Merci beaucoup

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

Géométrie dans l'espace : pyramide, cône et sphère en quatrième
5 fiches de mathématiques sur "Géométrie dans l'espace : pyramide, cône et sphère" en quatrième disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

20 visiteurs

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

Patron d'un tétraèdre trirectangle

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths