Inscription / Connexion Nouveau Sujet
petit problème
bonjour,
j'ai un exercice à faire sur un chapitre: "la trigo" qu'on a jamais abordé en cours.
Voilà l'énoncé:
dire à chaque fois si c'est vrai ou faux et justifier,
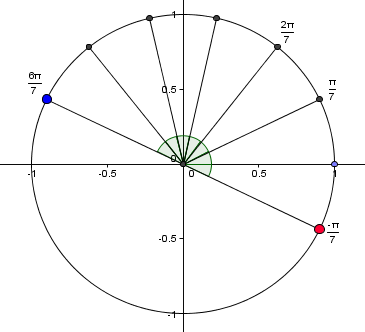
a) -pi sur 7 et 6pi sur 7 ont même point image sur le cercle trigonométrique
b) pour tout nombre réel x, sin(x-10pi)=sin x
c)il n'existe pas de réel x tel que sin x+ cos x =0
d) pour tout nombre réel x, (cos x)²+ (sin x)²=1
e) l'équation sin x=0,3 a une unique solution dans l'intervalle (0;2pi)
f)l'équation sin x=-1 a une solution unique dans l'intervalle (-pi; pi)
Merci pour votre réponse, il est bien évident que je continue à chercher de mon côté,
ps: je suis nouveau, je m'appelle Clément et je passe en 1ère S
Bonjour,
Ton cours + une représentation géométrique
sur le cercle trigonométrique devrait faire l'affaire,
Alain
C'est très sympathique de m'avoir répondu mais est ce que quelqu'un pourrais me donner une réponse plus complète avec des coups de pouce au moins pour chaque question
Merci
a) As-tu dessiné un cercle trigonométrique et placé dessus les angles - pi/7 et 6pi/7 ? Il est alors facile de répondre.
b) Observe qu'on a 10pi = 5*2pi.
c) La condition peut s'écrire sin x = - cos x. Essaie de trouver sur le cercle trigonométrique des points correspondant à un sinus et à un cosinus de signes opposés. Parmi ces points y en a-t-il au moins un pour lequel on aurait |sin x| = |cos x| ?
Pour la question b) , inspire-toi de ce que Priam t'a indiqué . Ajouter ou retrancher 2
( ou un multiple de 2 ) à un angle, c'est à dire un ou des tours complets , va te ramener au même point sur le cercle trigonométrique . Donc égalité pour sin et cos .
A retenir : 2 = 1 tour complet
Annuler
connectez vous