Inscription / Connexion Nouveau Sujet
point d'inflexion
Bonjour, je voudrais savoir si l'exo que j'ai fais est juste et si quelqu'un pouvais m'aider pour la fin. Merci
soit f(x)=0.125x3-0.75x²+4 sur [0;5]
1.trouver f'(x)
2.Trouver sens de variation de f
3.Démontrer que la courbe C admet un point d'inflexion. (préciser coordonnées)
4.Déterminer l'équation de sa tangente en ce pt.
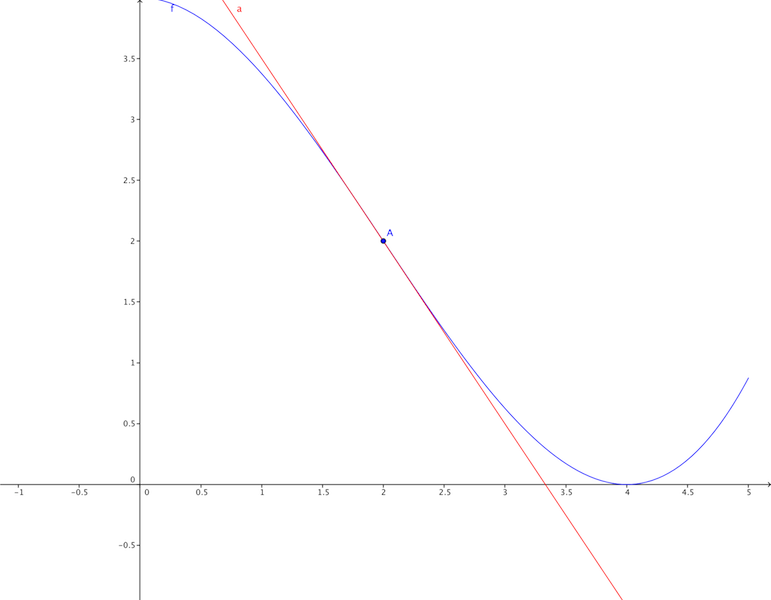
5.Construire la courbe et la tangente.
J'ai trouver :
1. f'(x)=0.375x²-1.5x
2. que la fonction est décroissante sur [0;4]et croissante sur [4;5]
3. J'ai calculer f''(x) et j'ai trouver 0.75x-1.5
Elle s'annule en 2 donc 2 est le pt d'inflexion.
f(2)=2 donc les coordonnées sont (2;2)
C'est ça pour l'instant ?
Bonsoir,
C'est presque ça.
en fait le point d'inflexion est bien 2 mais tu ne l'as pas prouvé !
il ne suffit pas que la dérivée seconde s'annule ! encore faut-il qu'elle change de signe !
Par exemple la courbe y = x4 qui ressemble à une parabole avec le sommet "un peu écrasé" a bien sa dérivée seconde y" = 12x2 qui s'annule en 0, mais elle ne change pas de signe : pas de point d'inflexion.
Prouver ici que la dérivée seconde change de signe est facile : tu as juste une phrase à ajouter
D'accord merci.
Mon équation de tangente :
Y=f'(2)(x-2)+f(2)
f'(2)=-1.5
f(2)=2
Y=-1.5(x-2)+2
=-1.5x+5
Juste ?
Annuler
connectez vous