Inscription / Connexion Nouveau Sujet
Points non alignés sur un cube, le démontrer ?
Bonjour et merci de l'intérêt porté à ce post.
Je suis sur un exercice de Maths où je dois créer un cube et y placer 4 points I J K sur les arrêtes de manière à ce qu'ils ne soient absolument pas alignés.
Il faut que 2 points soit joignables entre eux.
Et je dois démontrer que les points ne sont pas alignés + tracer l'intersection de I J K.
Déjà, voici ma figure sous géogébra : http://***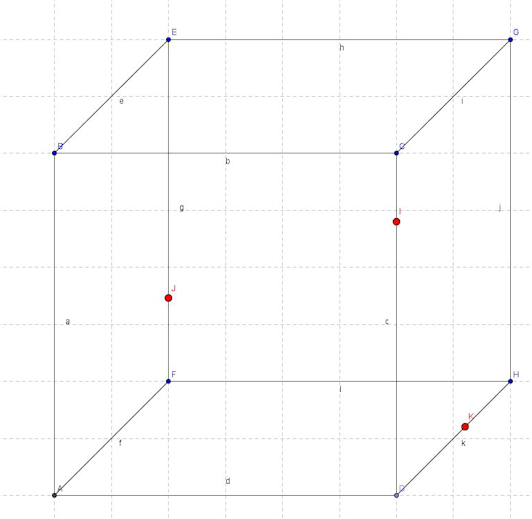
* Tom_Pascal > image placée sur le serveur de l'
, merci d'en faire autant la prochaine fois Razer... *
Je ne sais absolument pas comment faire quelqu'un pourrait m'aider s'il vous plaît ???
Bonjour,
1) déja "ça" ce n'est pas ton énoncé, ce que tu dis ici n'a aucun sens, recopie le vrai avec les vrais mots qui sont dedans.
2) (edit : ce point 2 saute, déja dit par Tom_Pascal)
3) sur ta figure les points I J K ne peuvent jamais être alignés car cela voudrait dire que déja le point K est dans le plan (DFEC) si tant est qu'on lise correctement tes noms de points (les noms on les déplace pour qu'il soient lisibles et pas cachés par les traits du dessin, traits dont l'affichage du nom "Geogebra" est d'ailleurs inutile)
4) "Il faut que 2 points soit joignables entre eux". formulation sans aucun sens, voir point 1.
deux points sont toujours "joignables" par définition de la droite entre deux points.
pareil pour "l'intersection de I J K" ça ne veut rien dire
une intersection c'est entre deux objets
on peut deviner peut-être que, ma fois, il pourrait peut être s'agir de l'intersection du plan (IJK) avec va savoir quoi ? les faces du cube ? un des plans qu'on peut définir par ces 8 sommets ? une droite ? laquelle ?
bref là aussi voir point 1.
Annuler
connectez vous