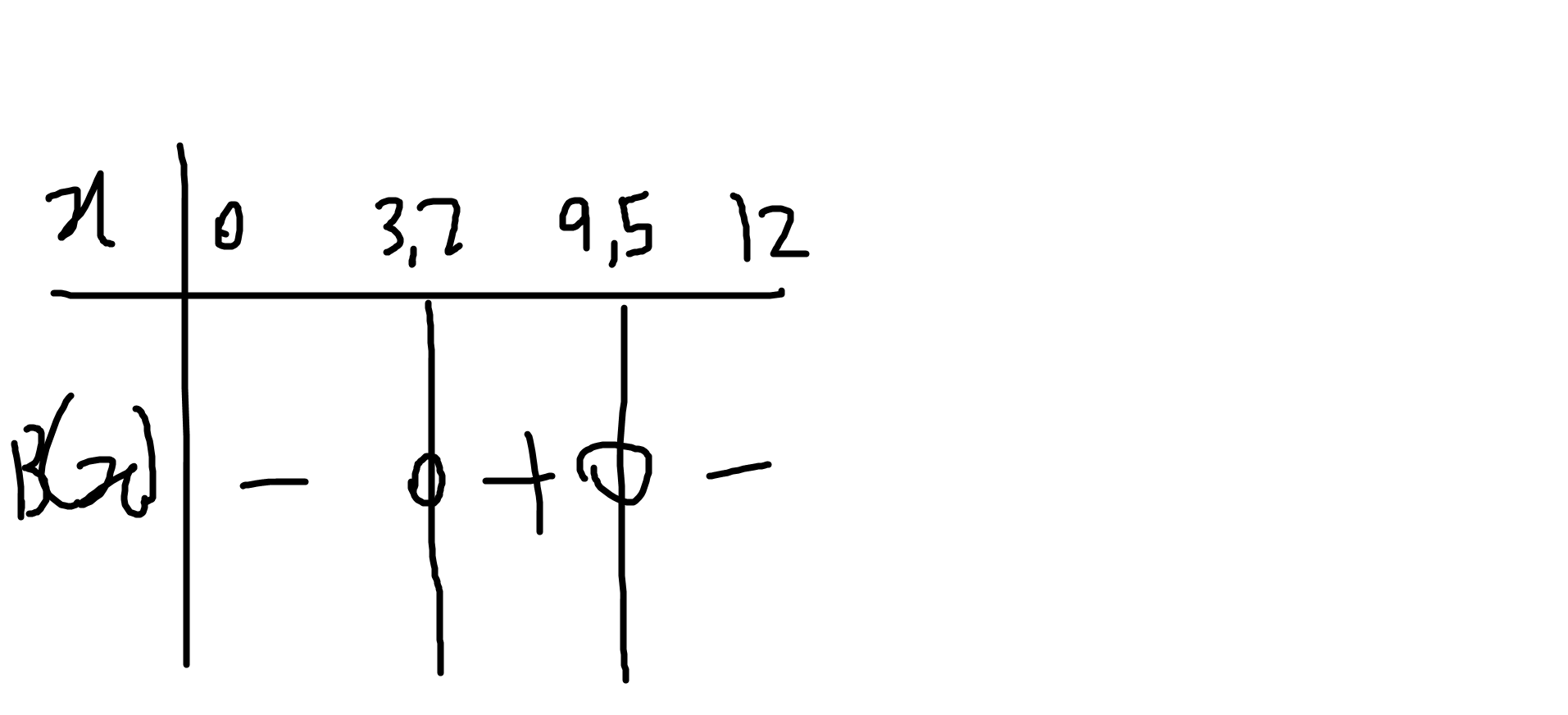Inscription / Connexion Nouveau Sujet
4a) B(x)=R(x)-C(x)= 7x-(0.6x²-0.62x+18.24)
=7x-0.6x²+0.62x-18.24
=-0.6x²+7.62x - 18.24 --- c'est -18.24
ok
continue
c'est ça, sauf que les bornes ne sont pas les infinis
quel est l'ensemble de définition de B ?
puis calcule l'image de ses bornes
j'ai pas compris l'ensemble de définition de B
sinon
B(0) = -0.6*0²+7.62*0-18.24 = -18.24
B(12) = -0.6*12²+7.62*12-18.24 = -13.2
4. On note B(x) le bénéfice mensuel,...
(a) Montrer que, pour tout x dans l'intervalle [0; 12] : B(x) = −0, 6x² + 7, 62x − 18, 24
sur le tableau de variation de B, à la ligne des x, il y a donc 0 et 12 à la place des infinis
et dessous ces bornes, tu notes leur image (-18.24 et -13.2, oui)
(c) Résoudre l'équation B(x) = 0. Interpréter le résultat avec le contexte de l'exercice.
(d) Etudier le signe de la fonction B sur [0; 12].
tu sais faire ?
sinon ![]() 3-Fonctions du second degré : équations, signe et inéquations
3-Fonctions du second degré : équations, signe et inéquations
4c) −0, 6x² + 7, 62x − 18, 24 = 0
= (-0.6x) (-0.6x) +7.62x = 18.24
= 3.6x+7.62=18.24
=11.22x = 18.4
= x= 1.64
je pense pas que c'est ca
ah non, ce n'est pas ça.
il s'agit d'une équation du second degré, forme ax² + bx + c = 0
ici, a = ...?
b = ...?
c = ...?
quelles méthodes as-tu apprises en classe pour résoudre ce type d'équation ?
4c) a= -0.6 b= 7.62 c= -18.24
on utilise delta? si oui alors
delta= 7.62²-4*(-0.6)*(-18.24) = 14.29 Il y 2 solutions réelles
x1 = -7.62+√14.29 sur 2*(-0.6) = 3.2
x2 = -7.62-√14.29 sur 2*(-0.6) = 9.5
on pourrait utiliser la factorisation de la forme canonique (puisqu'on a alpha et beta),
mais ici, avec des nombres arrondis, on préfèrera le discriminant delta.
tes racines sont exactes : 3.2 et 9.5
ce qui me dérange un peu, ce sont les valeurs approchées de delta;
dans une résolution d'équation, on garde les valeurs exactes jusqu'à la fin.
interprétation de 3.2 et 9.5 dans le contexte ?
D'accord donc
delta= 7.62²-4*(-0.6)*(-18.24) = 14.2884 Il y 2 solutions réelles
x1 = -7.62+√14.29 sur 2*(-0.6) ≃ 3.2
x2 = -7.62-√14.29 sur 2*(-0.6) ≃ 9.5
3.2 et 9.5 c'est l'intervalle de x pour que son bénéfice soit positif
environ égal aussi pour delta, ce serait parfait.
alors,
pour l'équation B(x) = 0, ce n'est pas la bonne interprétation
3.2 et 9.5 sont les racines de B (tu as lu la fiche indiquée?)
ce sont les abscisses des points d"intersection entre la courbe de B et l'axe des abscisses.
ça correspond donc aux quantités produites qui ....? le bénéfice
trace la courbe de B pour visualiser
3.2 et 9.5 c'est l'intervalle de x pour que son bénéfice soit positif ------ ça c'est (presque) juste !
mais c'est la réponse à la 5a)
3.2 et 9.5 sont les bornes de l'intervalle ---> comment tu écris l'intervalle ?
ça correspond donc aux quantités produites qui augmente le bénéfice
3.2 et 9.5 sont les bornes de l'intervalle 6.35 donc [ 3.2; 9.5] ?
ah mais la
4c) 3.2 et 9.5 sont les racines de B. Ce sont les abscisses des points d'intersection entre la courbe de B et l'axe des abscisses.
4d)
5a) l'intervalle x est donc [ 3.2; 9.5]
4.
(c) oui, mais va au bout du raisonnement
pour x=3.2 ou x=9.5 le bénéfice est .....?
(d) Etudier le signe de la fonction B sur [0; 12].
==> voir cours
tu as appris la règle des signes du trinôme ?
si non, factorisation
puis tableau de signes
![]() 3-Fonctions du second degré : équations, signe et inéquations
3-Fonctions du second degré : équations, signe et inéquations
5a) oui
4c) 3.2 et 9.5 sont les racines de B. Ce sont les abscisses des points d'intersection entre la courbe de B et l'axe des abscisses. pour x=3.2 ou x=9.5 le bénéfice est positive
mais non !
puisque ce sont les racines de B, elles annulent B(x)
donc pour ces 2 valeurs, le bénéfice est nul
4d) j'ai oublié
5a) le nombre d'article que l'entreprise doit produire et vendre pour réaliser un
bénéfice mensuel positive est que le nombre d'article x soit dans l'intervalle [ 3.2; 9.5]
5b) le nombre d'article que l'entreprise doit produire et vendre pour réaliser un
bénéfice mensuel maximal est 6.35 car son bénéfice serait de 5950€
ah mince
4c) 3.2 et 9.5 sont les racines de B. Ce sont les abscisses des points d'intersection entre la courbe de B et l'axe des abscisses. pour x=3.2 ou x=9.5 le bénéfice est positive
4c) 3.2 et 9.5 sont les racines de B. Ce sont les abscisses des points d'intersection entre la courbe de B et l'axe des abscisses. pour x=3.2 ou x=9.5 le bénéfice est nul*
4d) Si Delta > 0, P(x) a le signe de a à l'extérieur des racines et le signe de (- a) entre les racines. ca doit etre ca non??
oui, donc refais ça en appliquant correctement la règle du signe que tu as citée
ah donc
entre 0 et 6.35 c'est -
et 6.35 à 12 c'est aussi -
Donc si j'ai tout bien réussi c'est ca :
1) R(x) = 7x
2) bénéfice de mai = R(4) - C(4) = 4 * 7 - (0.6 * 4² - 0.62 * 4 + 18.24) = 2.64k€
bénéfice de juin = R(6.5) - C(6.5) = 6.5 * 7 - (0.6 * 6.5² - 0.62 * 6.5 + 18.24) = 5.94k€
Le bénéfice en juin a était très important au mois de juin car le bénéfice en mai était de 2640€ et en juin le bénéfice était de 5940€ l'équivalent de 3300€ de différence
3)
a/L'intervalle dans lequel doit se situer x pour que le bénéfice mensuel réalisé soit positif est [ 3;9.5]
b/ la valeur de x pour laquel le bénéfice mensuel est maximal est 6 vu que la courbe C et R sont le plus éloigner
4a) B(x)=R(x)-C(x)= 7x-(0.6x²-0.62x+18.24)
=7x-0.6x²+0.62x-18.24
=-0.6x²+7.62x+18.24
b/
alpha = -7.62/2*(-0.6) = 6.35
béta = -0.6*6.35²+7.62*6.35-18.24 = 5.95
+ le tableau de variation a rajouter
c/
a= -0.6 b= 7.62 c= -18.24
delta= 7.62²-4*(-0.6)*(-18.24) = 14.2884 Il y 2 solutions réelles
x1 = -7.62+√14.29 sur 2*(-0.6) ≃ 3.2
x2 = -7.62-√14.29 sur 2*(-0.6) ≃ 9.5
3.2 et 9.5 sont les racines de B. Ce sont les abscisses des points d'intersection entre la courbe de B et l'axe des abscisses. pour x=3.2 ou x=9.5 le bénéfice est nul
d/ tableau de signe a faire
5a) le nombre d'article que l'entreprise doit produire et vendre pour réaliser un
bénéfice mensuel positive est que le nombre d'article x soit dans l'intervalle [ 3.2; 9.5]
5b) le nombre d'article que l'entreprise doit produire et vendre pour réaliser un
bénéfice mensuel maximal est 6.35 car son bénéfice serait de 5950€
Donc si j'ai tout bien réussi c'est ca :
1) R(x) = 7x
2) bénéfice de mai = R(4) - C(4) = 4 * 7 - (0.6 * 4² - 0.62 * 4 + 18.24) = 2.64k€
bénéfice de juin = R(6.5) - C(6.5) = 6.5 * 7 - (0.6 * 6.5² - 0.62 * 6.5 + 18.24) = 5.94k€
Le bénéfice en juin a était trèsplus important au mois de juin car le bénéfice en mai était de 2640€ et en juin le bénéfice était de 5940€ l'équivalent de 3300€ de différence
3)
a/L'intervalle dans lequel doit se situer x pour que le bénéfice mensuel réalisé soit positif estsemble être [ 3;9.5]
b/ la valeur de x pour laquelle le bénéfice mensuel est maximal est semble être 6 vu
que la courbe C et R sont le plus éloigner
4a) ok
b/
alpha = -7.62/2*(-0.6) = 6.35
béta = -0.6*6.35²+7.62*6.35-18.24 = 5.95 ---- mets
 , c'est un arrondi
, c'est un arrondi
+ le tableau de variation a rajouter
c/ oui
d/ tableau de signe a faire
5a) oui
5b) le nombre d'article que l'entreprise doit produire et vendre pour réaliser un
bénéfice mensuel maximal est 6.35 caret son bénéfice serait est alors de 5950€
---- important : explique que d'après l'étude de la variation (tableau), la fonction admet un maximum

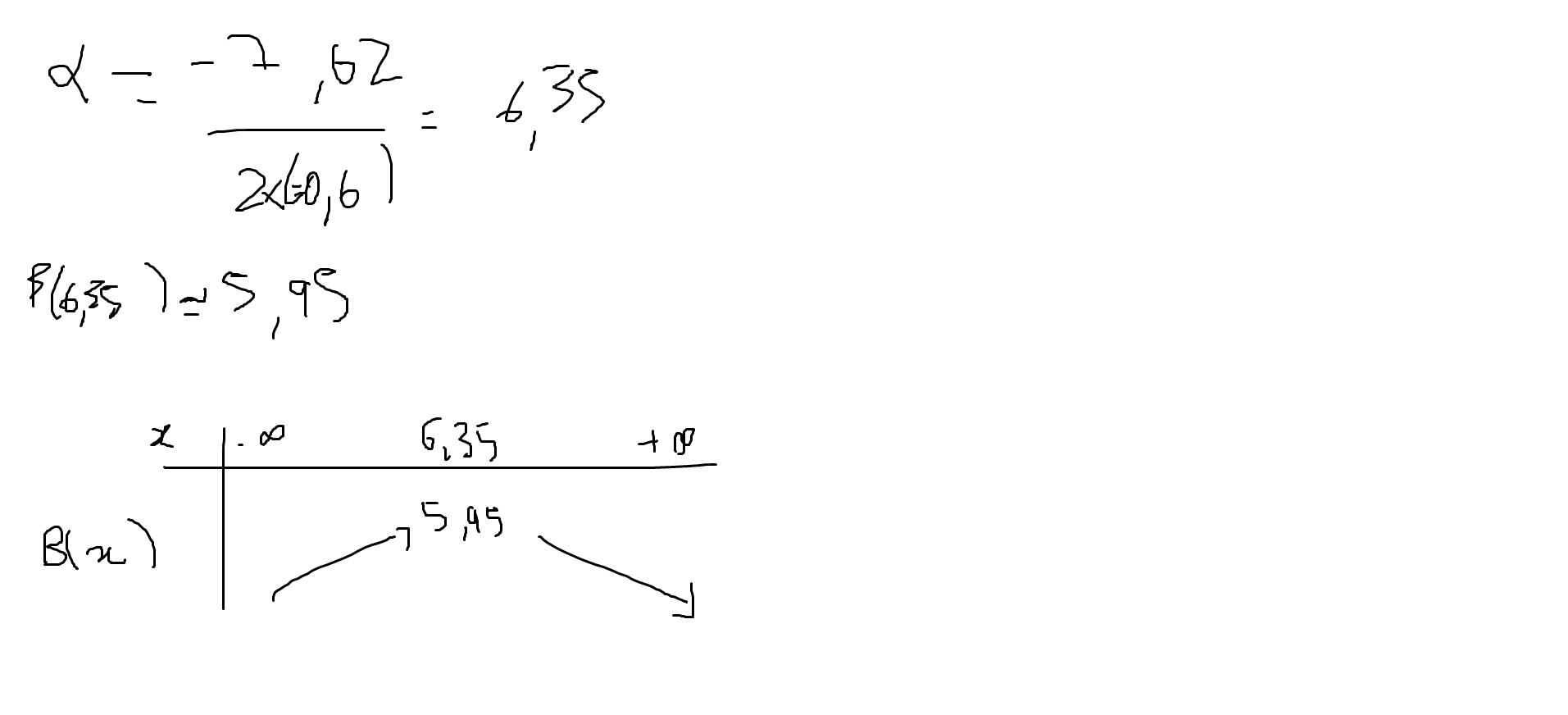
 , l'abscisse du sommet
, l'abscisse du sommet