- Arithmétique dans Z - supérieur
- Exercice : le petit théorème de Fermat
- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
Preuve par induction d'une sommation
Salut,
J'arrive par à solution une preuve par induction d'une sommation, pourriez-vous m'aider ?
Pour tout entier n strictement positif
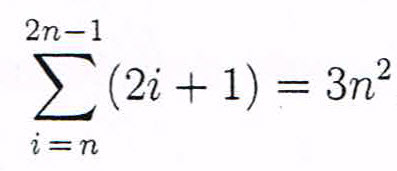
Bonjour,
Je pense, que tu sais prouver que l'égalité est vraie pour les premiers termes de la suite Un =  (2i+1) (pas pratique à écrire avec cet éditeur)
(2i+1) (pas pratique à écrire avec cet éditeur)
si tu calcules ensuite (Un+1) - (Un) =  ... -
... -  ...
...
tu devrais trouver que la différence est [-(2n+1) + (2(2n)+1) + (2(n+1)+1)]
tu développes et réduis, tu ajoutes (Un) qui vaut 3n^2 et tu devrais trouver 3(n+1)^2
Bonjour.
@PerArgal.
Je viens juste de me mettre au LaTeX (5 semaines). C'est rébarbatif au début mais on s'y fait. Téléchargez le guide Latex ou imprimez le (3 pages) pour l'avoir sous la main en cas de besion
je vais juste vous reprendre mais en LaTeX en gardant la notation originale et en posant
.
je vous donne ci-dessous le code LaTeX en renommant les balises entre crochets "tex" par "bbb" (en gras souligné). l'expression a été décomposée en 4 blocs chacun écrit avec une couleur et de taille croisssante,le 3ème bloc est repris en bleu piur une meilleure lecture à l'écran. Les balises pour le gras et le souligné ne font partie du LaTeX et n'apparaissent pas à l'écran. Elles ont été utilisées pour l'affichage
[bbb]3${\blue{S_{n+1}=\sum_{i=n+1}^{2(n+1)-1}u_i}}[/bbb]
[bbb]3${\red{=\sum_{i=n+1}^{2n+1}u_i}=-u_n+\sum_{i=n}^{2n+1}u_i[/bbb]
[bbb]4${\green{=\sum_{i=n}^{2n-1}u_i-u_n+u_{2n}+u_{2n+1}}}}[/bbb]
[bbb]4${\blue{ =\sum_{i=n}^{2n-1}u_i-u_n+u_{2n}+u_{2n+1}}}}[/bbb]
[bbb]5$=3n^2-u_n+u_{2n}+u_{2n+1}=......}[/bbb]
Bon courage pour le LaTeX et allez-y.
MERCI!!!
C'est trop beau... Je sévis depuis récemment et essentiellement sur l'île des sciences physique, mais ce genre de souplesse commençait à me manquer sérieusement ....
Mais au fait ... le guide latex ... de 3 pages ... on le trouve où?
salut
pour info ::: à droite de l'ancre un petit parchemin ... on clique dessus et trouve le trésor ....
@uruo
Désolé pour ton post
Cela ne pouvait être qu'un épicurien pour faire cette remarque (le trésor est à portée de main si l'on accepte de ne pas regarder trop loin)... sauf que l'ancre ... elle est où?
Bon, j'admets la possiblité d'être idiot, puisque je serais déjà bien incapable de démontrer scientifiquement que ce post existe ... (ce qui pourrait être l'objet d'un autre post d'ailleurs)
Bonjour.
@PerArGal
Ne t'énerves pas. Carpediem a juste voulu faire de l'humour.
Pour le lien c'est l'icône  à droite dans la bande orange, et en disant ça j'ai peur de te froisser et encore plus si je disais voir
à droite dans la bande orange, et en disant ça j'ai peur de te froisser et encore plus si je disais voir ![]() [lien]
[lien]
@delta-B, @carpe diem
Enervé point du tout n'étais je (*) ... simplement amusé (au sens premier) de la formulation utilisée par Carpe diem ...
(*) je ne le suis jamais ...
Bonjour
la récurrence était imposée ? parce que ça va aussi vite de reconnaitre la somme de n termes de la suite arithmétique de raison 2 et de premier terme 2n+1, dernier terme 4n-1, donc somme = nombre de termes fois moyenne entre le premier et le dernier terme = n(3n) = 3n² ....
Il me semble que l'objet de l'exercice était l'utilisation de la récurrence. En tout cas c'est comme cela que j'interprète le titre ...
Merci bcp à vous tous pour les explications, c'est vrai en fin de compte je dois trouver (3n2+6n+3) équivalente pour n+1 dans 3(n+1)2=3n2+6n+3. mais je ne comprends pas toujours comment on a pu sortir la formule :
Merci encore pour votre aide.
Bonjour.
@uruo
Du moment que j'en suis l'auteur c'est à moi de répondre.
1) Première somme en bleu: C'est la définition de Sn+1 puis j'ai simplifié l'écriture de la borne supérieure de la la somme.
2) j'ai ajouté à la somme eu rouge le terme un pour qu'elle commence à l'indice n (borne inférieure de de Sn), il fallait donc aussi retrancher un.
3) j'ai extrait de la 2ème somme en rouge les terme d'indice supérieur à 2n-1 pour faire apparaître Sn, les termes extraits sont u2n et u2n+1 et j'ai utilisé l'hypothèse de récurrence Sn = 3n2.
Un grand merci spécial à vous @delta-B, désolé si ta réponse t'appris le temps pour l'écrire, mais après mis mon message pour la formule j'ai essayé de la comprendre et j'ai trouvé la relation entre les bornes de la sommation et les éléments ajoutés. votre effort et très remarquables, tout mon respect pour vous. Et je remercie aussi les autres qui ont répondu à mon message. Merci à tous.




 arithmétique en post-bac
arithmétique en post-bac