Inscription / Connexion Nouveau Sujet
primitive
Bonjour,
j'ai un exo sur les integrals et primitives et je voudrais demander votre aide...
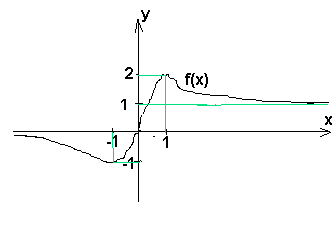
On connaît pas f mais on a son tableau de variations:
sur ]-00; -1] f(x) decroît lim en -00 est 0, f(-1)=-1
sur [-1;1] f(x) croît; f(0)=0 et f(1)=2
sur [1; +00] f(x) decroît lim en +00 est 1
1/ J'en déduis alors que f(x)<0 qd x<0 et f(x)>0 qd x>0
Donc Fdecroît qd x<0 et croît qd x>0
Mais 2e et 3e questions me^posent plus de problèmes...
2/ Il faut trouver a et b positifs tels que
3/ il faut trouver lim de F(x) en +00
merci en avance
Bonjour
Fais un tableau de variation de f(x), sa va te donner les extremums, et avec sa tu devrait pouvoir encadrer F(x) ( pense aussi a utiliser le théorème de l'encadrement )
oui, j'ai un min de f(x) en -1 et un max en 1 mais j'en conclue quoi? Je sais même pas la valeur de F(2)...
Esquisse de ce que pourrait être f(x) sur le dessin (cela aide à réfléchir).
Pour x dans [0 ; 2], on a 0 <= f(x) <= 2
0 <= S(de 0 à 2) f(t) dt <= S(de 0 à 2) 2. dt
0 <= S(de 0 à 2) f(t) dt <= 4
a = 0 et b = 4 (qui sont bien positifs (même 0))
-----
Comme f(x) >= 0 pour x dans [0 ; 2]
et f(x) > 1 pour x dans ]2 ; oo[
lim(x -> oo) F(x) = oo
En effet lim(x -> oo) F(x) = S(de0à1) f(t) dt + S(de 1 à oo) f(t) dt
et comme S(de0à1) f(t) dt >= 0
On a lim(x -> oo) F(x) >= S(de 1 à oo) f(t) dt
et comme f(t) > 1 sur [1 ; oo[, on a:
lim(x -> oo) F(x) >= S(de 1 à oo) 1. dt
lim(x -> oo) F(x) >= [t](de 1 à oo)
lim(x -> oo) F(x) >= oo
et donc lim(x -> oo) F(x) = oo
-----
Sauf distraction. 
Annuler
connectez vous