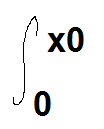bonjour

c'est correct

Salut,
Pourtant, c'est bien ça...
Qu'est-ce qui te pose problème ?

Bonjour,
UNE primitive
F(x)=\frac{-1}{0,2}e^{-0,2x}+C=-5e^{-0,2x}+C

  Bonjour  Yzz

Bonjour,
Tu as peut-être oublié de rajouter une constante arbitraire à ta primitive.
Sinon, on ne te demande pas de trouver la primitive car il y en a une infinité.
Celle que tu donnes convient ; elle correspond à la formule [e^(ax+b)]/a avec b = 0 .
Mais [e^(-0.2x)]/(-0.2) + 2013 convient aussi !

Bonjour tous !
RideauMan quel succès

Ah oui, car n'importe quel nombre u devient 0 lorsqu'on dérive.. Merci de vos réponses !

Le problème est que je calcule une aire, exprimant un "surplus des consommateurs". Lorsque je remplace les nombres dans la primitive et que je fais la soustraction des deux, je trouve un résultat négatif.. Faut il le transformer en résultat positif?

En l'occurence, mes deux nombres sont 2,6 (en haut) et 0 (en bas).
Mon expression complète (dont je dois trouver une primitive) est 100e(-0,2x)-150.
Pour la primitive, j'ai trouvé ceci : 100*e(-0,2)-150x

En remplacant par 2,6 je trouve: -687,26
En remplacant par 0, je trouve: 100.
La différence des deux fait donc -587,26..

Ta primitive est fausse.

Il faut perdre l'habitude d'écrire "la" primitive ; écris "une" primitive.
Avec g(x) = 100 e^-0,2x - 150 , une primitive G est définie par G(x) = 100 - 150x = -500 e^-2x - 150x .

Je vais reprendre l'exercice depuis le début..

Un téléviseur est mis en vente sur le marché:
La fonction d'offre associe au nombre d'exemplaires x le prix à l'unité auquel les producteurs sont prêts à vendre: elle est définie par f(x)=25e^(0.3x)
La fonction de demande associe le prix à l'unité que les clients sont disposés à acheter: elle est définie par g(x)=100e^(-0,2x)

1) a) Etudier le sens de variation de f, tracer sa courbe dans un repère.
     Pour cela, j'ai calculé la derivée. Je trouve f'(x)=25*0,3x*e^(0,3x): la derivée est positive donc la fonction est croissante. J'ai calculé f(0), f(1), f(2), f(3) et f(4), et j'ai tracé cette courbe dans mon repère.


b)Etudier le sens de variation de g, tracer sa courbe dans un repère.
     J'ai également calculé la derivée. Je trouve 100-0,2e^(-0,2x): la derivée est négative donc la fonction est décroissante. J'ai calculé g(0), g(1), g(2), g(3) et g(4), et j'ai tracé cette courbe dans mon repère.

2 Le point d'intersection des deux courbes (prix de l'offre = prix de la demande) correspond à l'équilibre du marché. Determiner les coordonnés (x0 y0) de ce point .
     Grace à mon schéma, j'ai trouvé 2,7 en abscisse et 57,3 en ordonnée.

j'en suis ici...
3 A Pour x appartenant à [0;x0], les acheteurs sont prêts à acheter plus cher que le prix d'équilibre y0. Les économies du consommateur dont appelées "surplus du consommateur", et est égal à |x0 0 (voir image)g(x)dx-x0-y0. Calculer ce surplus.

     J'ai donc cherché une primitive. Elle serait donc -500e^(-2x)-(2,7*57,3)x = 500e^(-2x)-154x. Je choisis de calculer F(x0) qui est F(2,7). Je trouve -407,3. Je calcule F(0, je trouve -500.
F(x0)-F(0) = 93. C'est positif! Ca correspond donc au surplus des consommateurs?

Merci d'avoir eu la peine de lire..

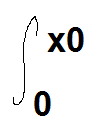
Tu peux trouver la valeur exacte de x₀ en résolvant f(x) = g(x) :
25 e^0,3x = 100 e^-0,2x.
e^0,3x = 4 e^-0,2x.
e^0,3x e^0,2x = 4 e^-0,2x e^0,2x
e^0,5x = 4
0,5 x = ln4
x = 2 ln4

D'où vient le 154x dans ta primitive ?

Je n'ai pas encore étudié les logarithmes naturels.. Merci tout de même pour la résolution de l'inégalité!
Le 154 correspond à 2,7*57,3.. Ce sont les points d'intersection de la courbe

Merci pour ces conseils!

@Sylvieg : comment est il possible de trouver la valeur exacte de y0..?

J'aurai besoin de savoir la valeur exacte de y0, sachant x0 et les fonctions définissant les deux courbes.

-500 e^-0,2x - 150x

100 = -100 = -1005 = -500

Pour y₀, rien de palpitant :

y₀ = g(x₀) = 100e^-0,2x0 = 100e^-0,4ln4 = 100(e^ln4)^-0,4 = 1004^-0,4 .

4^-0,4 n'est pas vraiment agréable

y₀ 57,43 ; ce n'est pas très loin de ton 57,3

Pour l'intégrale, je n'arrive pas à comprendre ce que tu as écrit.
Est-ce "(intégrale de 0 à x₀ de g(x)dx ) - x₀ - y₀" ou "intégrale de 0 à x₀ de (g(x)- x₀ - y₀)dx " ?

C'est écrit tel quel: (image) g(x)dx-x0y0
J'an ai donc déduit qu'il fallait calcluler l'intégrale de toute l'expression..

Merci pour y0 !!

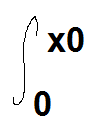
Il faut peut etre trouver une primitive pour la premiere partie de l'expression? Et ensuite soustraire x0-y0 ? Cela changerait tout..

J'ai opté pour faire uniquement la primitive de g(x) et ensuite soustraire y0 et y0. Ca a l'air satisfaisant dans mes résultats.

Il me reste la même chose pour le surplus des producteurs, définit par : x0y0-(image)f(x)dx.
Sachant que f(x) est 25e(0,3x)
Jai trouvé une primitive: 25*(1/0,3)e(0,3x).
Je calcule donc F(x0), je trouve environ -32
Je calcule F(0), je trouve environ 75.
-32 - 75 fait -107.. C'est faux car le surplus des producteurs doit être positif..
Help..

(voici limage)

J'ai terminé mon DM, il me semble juste, merci pour ces précisions

Je précise ce que j'ai compris pour les deux calculs.

Surplus des consommateurs : G(x0) - G(0) - x0y0

surplus des producteurs : x0y0 - ( F(x0) - F(0) ) = x0y0 - F(x0) + F(0)

Bravo pour ta ténacité.

J'ai pu comprendre l'exercice et je serai capable de le refaire, merci de votre aide!