Inscription / Connexion Nouveau Sujet
primitives
Bonjour, pourriez vous m'apporter votre aide pour l'exercice suivant :
On donne dans le repère (0, i, j) ci dessus, les courbes (C1), (C2), (C3) représentant respectivement trois fonctions f1, f2 et f3 définies et dérivables sur R.
Exceptée l'ordonnée du point H qui est 1/4, les coordonnées des points O, A, B, C, D, E, F, G sont entières. De plus, les tangentes en C et H à la courbe (C1), la tangente en F à la courbe (C2) et les tangentes en E et G àla courbe (C3) sont parallèles à l'axe des abscisses.
1° Etablir par lecture graphique le tableau de signes et le tableau de variations de chacune des fonctions f1, f2 et f3.
2° Les fonctions f1, f2 et f3 sont en fait une fonction f, sa dérivée f' et l'une des primitives F.
A l'aide de la question précédente, déterminer la courbe représentative de chacune des fonctions f, f' et F.
Merci de votre aide.
Bonsoir,
Je prends le relai appremment plus personne n'est là ...
Pense toujours au lien: signe de la dérivée correspond au sens de variation de la fonction.
au temps pour moi
est la courbe représentative de
,
de
et
de
si l'on considère les trois courbes une seule , , est décroissante croissante
une seule des fonctions est négative jusqu'à 0 et positive ensuite
ce qui voudrait dire
qu'elle pourrait être la dérivée d'une fonction décroissante jusqu'à 0 et croissante en suite
par conséquent ne peut-être que la courbe de la fonction dérivée
Bonsoir philgr22 je vous laisse poursuivre ce n'est guère évident à expliciter
F est une primitive de la fonction f signifie que F'(x) = f(x)
Par conséquent les variations de la fonction se déduisent du signe de la dérivée de f
f3(x) semble être la primitive F
F est une primitive de la fonction f signifie que F'(x) = f(x)
Par conséquent les variations de la fonction se déduisent du signe de la dérivée de f
f3(x) semble être la primitive F
Dans ce cas ,quel serait ton choix pour les trois courbes?
Bonsoir à tous,
A mon avis, il est plus simple de regarder les points où les fonctions s'annulent et les points où les tangentes sont horizontales et de les mettre en correspondance.
brisco59 devrait commencer par compléter ses tableaux en y faisant apparaître ces éléments. Après quoi, vérifier la concordance avec les variations elles-mêmes.
Je ne sais pas si je suis très clair...
Si je suis Larrech, les points ou les fonctions s'annulent
(C1) : Elle s'annule en C pour x=0 : tangente horizontale
(C2) : Elle s'annule en F pour x= 2 : tangente horizontale
(C3) : Elle s'annule en G pour x=1 : tangente horizontale et en E pour x=3 !: tangente horizontale
Je pense qu'il vaut mieux eviter plusieurs pistes dans c genre d'exercice : laissons le terminer avec celle qu'il a choisie et on verra apres..
Si je suis Larrech, les points ou les fonctions s'annulent
(C1) : Elle s'annule en C pour x=0 : tangente horizontale
(C2) : Elle s'annule en F pour x= 2 : tangente horizontale
(C3) : Elle s'annule en G pour x=1 : tangente horizontale et en E pour x=3 !: tangente horizontale
Avec cette methode , tu dois faire le lien entre changementde sens de variation et changement de signe de la derivée.
Je dirais que selon le post it de 21h28 : f et F seraient les fonctions f1 et f2
Pour moi la dérivée serait la fonction f3, mais sans grande conviction.
C'est pour cela qe j'ai besoin de vos explications
F est une primitive de la fonction f signifie que F'(x) = f(x)
Par conséquent les variations de la fonction se déduisent du signe de la dérivée de f
C1 : changement de variations en C pour x=0
C3 : la fonction s'annule en x=0
Alors j'en déduis que F est la courbe C1
f : la dérivée : la courbe C3
Pouvez vous me donner des explications supplémentaires pour renforcer mon raisonnement
Elle est negative jusqu'à quelle valeur pour x?
Quelle fonction est decroissante dans le meme intervalle?
Donc la fonction C2 : négative sur 1 <x<3
La fonction C2 s'annule en D pour x=1 et en E pour x=3
la fonction C3 : changement de variation : G en x=1
et changement de variation en E en x=3
La fonction C2 : f'
Je t'aide un peu plus :
f3 est negative sur]- ;0]
;0]
f1 est decroissante dans le meme intervalle .
A quel lien entre les deux peut on penser?
Donc la fonction C2 : négative sur 1 <x<3
La fonction C2 s'annule en D pour x=1 et en E pour x=3
la fonction C3 : changement de variation : G en x=1
et changement de variation en E en x=3
La fonction C2 : f'
OUI.
Si je vous suit : F' = f
donc F : courbe C3 son signe est celui de F'
et f les variations donc la courbe C1
Ai-je compris?.
Si je vous suit : F' = f
donc F : courbe C3 son signe est celui de F'
et f les variations donc la courbe C1
Ai-je compris?.
C'est moi qui ne te suis pas bien là...

F a pour dérivée f qui a pour dérivée f' d'accord?
A partir de là quelle est ta conclusion pour les courbes?
Deux points importants
Le premier: F primitive de f  F'=f.
F'=f.
Le deuxieme , s'interesser aux intervalles communs entre sens de variation d'une fonction et signe de sa dérivée.
A titre d'exercice simple, tu peux essayer de construire une fonction constante ( droite parallelel à OX), une fonction affine et une fonction du second degré qui soient liées par la meme relation que dans cet exercice : F,f et f'.
F: C1
f' : C2
f: C3
Je pense
Une petite vérification s'impose...
Exceptée l'ordonnée du point H qui est 1/4, les coordonnées des points O, A, B, C, D, E, F, G sont entières.
en image , à prouver par calcul
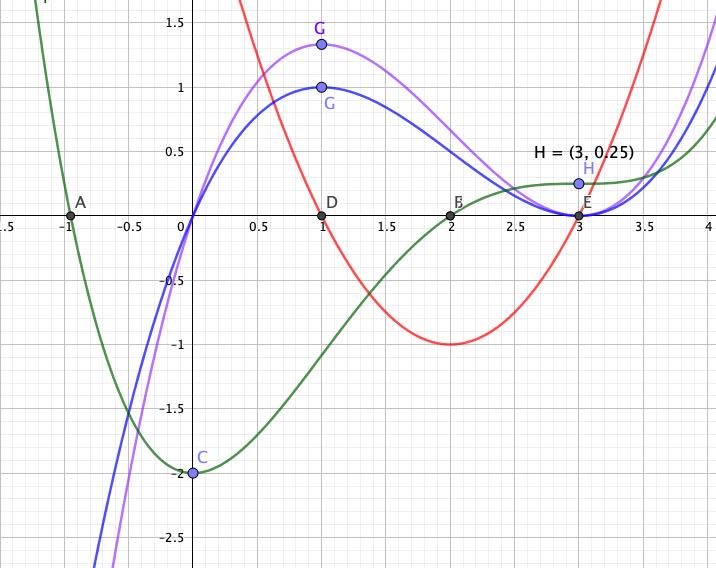
Si f' est représentée graphiquement par la courbe C2 , sachant que (D(1;0) E(3;0) et F(2;1)appartiennent à C2
alors
f'(2)=-1 =a(4-8+3) , et a=1
alors la primitive de f' telle que f(3)=0, puisque E est un point de la courbe C3 est la fonction f telle que
f
donc le point G(1,1) ne vérifie pas l'expression de f par conséquent la courbe C3 ne représente pas la fonction f ayant pour dérivée la fonction f' représentée par la courbe C2.
contrairement à l'énoncé
2° Les fonctions f1, f2 et f3 sont en fait une fonction f, sa dérivée f' et l'une des primitives F.
il ya une infinité de parabole qui passent par les points D et E...


