bonjour
j'ai un exercice de math qui me pose problème
un hôpital comporte 2 salles d'opérations s1 et s2 qui ont la même probabilité d'être occupées. La probabilité que l'une des salles ou moins soit occupée est de 0.9 ;celle que les 2 salles soient occupées vaut 0.5. Quelle est la probabilité
a)que la salle s1 soit libre ?
b)que les 2 salles soient libres?
c)que l'une des salles au moins soit libres?
d)qu'une seule salle soit libre?

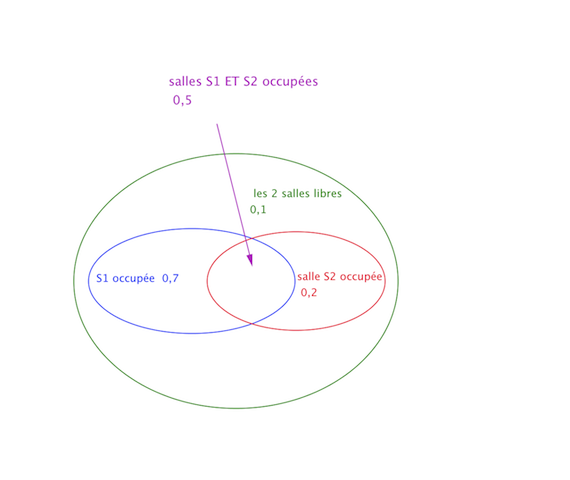
pour trouver les combinaisons possibles j'ai fait un tableau

s1 libre libre occupée occupée
s2 occupée libre libre occupée

pour la réponse du b) je pense que c'est la même probabilité que les 2 soient occupées soit 0.5

pour la c) je pense que c'est la même que pour la probabilité que l'une des salles au moins soit occupée c'est à dire 0.9
pour le a) je pense que c'est 0.75 de même que pour d)
pour une combinaison on a 0.5 alors pour 2 0.75

pourriez vous m'aider
merci