en quoi est-il "ouvert" ?

c'est l'application des deux relations

Je ne sais pas pourquoi est ce qu'il est ouvert.
Euh s'il vous plaît vous me pouvez juste me donner la réponse du A comme un exemple pour que je puisse faire le reste car je savais qu'il fallait utiliser ces deux formules mais je ne savais pas comment.
Merci d'avance.

En fait, ce n'est pas aussi simple qu'il n'y parait.
Les relations initiales ne suffisent pas.

Je te propose d'interpréter les conditions sous forme ensembliste.

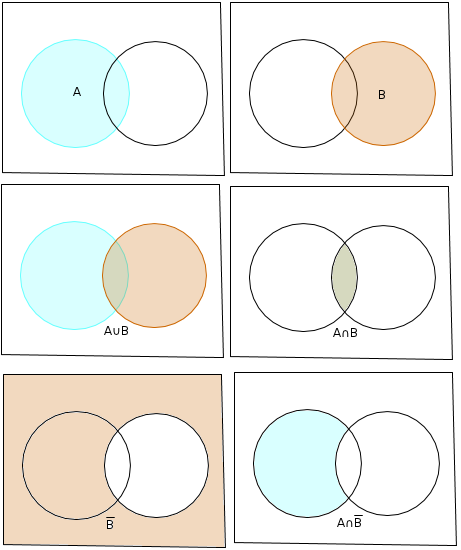
A est l'ensemble des événements qui réalisent la condition A
B est l'ensemble des événements qui réalisent la condition B
est l'ensemble des événements qui réalisent simultanément les conditions A et B : c'est l'intersection des ensembles A et B
est l'ensemble des événements qui réalisent l'une des deux conditions A ou B (sachant que les deux conditions peuvent être réalisées simultanément, quand on est dans l'intersection des deux) : c'est l'union des ensembles A ou B

est l'ensemble complémentaire de A, ce sont tous les événements qui ne réalisent pas A

p(A) est une mesure (comprise entre 0 et 1) de l'ensemble des événements qui constituent A

l'événement certain, p(E)=1, correspond à tous les événements possibles, E est parfois alors appelé l'univers
l'événement impossible, ou vide, correspond à quelque chose qui ne peut pas arriver, qui équivaut à l'ensemble vide.

Entraînons-nous :
Interprétation de la relation

si on considère p(A)+p(B), on ajoute la mesure de A et celle de B
ceci dit, on a du coup ajouté deux fois celle de leur intersection, , une fois avec p(A), une fois avec p(B)
c'est pourquoi, si on veut une mesure de , on ajoute p(A) et p(B), mais on retranche une fois la mesure de l'intersection pour compenser

Comment maintenant interpréter
il s'agit de mesurer l'ensemble des événements qui sont dans A mais pas dans B, donc on prend la mesure de A, de laquelle on retranche les événements qu'on aura comptés en trop, ceux de l'intersection de A et B


visualisation :

donc avec tes données numériques :

dernier exemple :

interprétation :
on veut mesure l'union de l'extérieur de A et de l'extérieur de B
cela donne ceci :


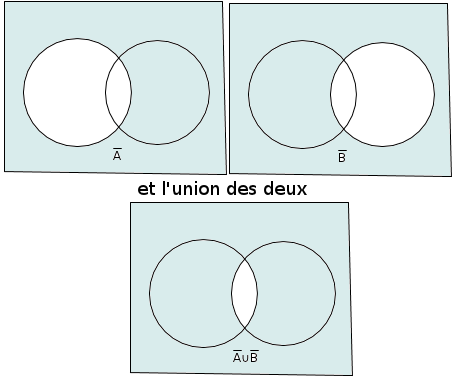
alors cette quantité est la mesure du tout, de l'univers (1), auquel on retranche l'intersection.

On pourrait aligner des pages de théories pour justifier tout cela formellement, je ne pense pas que ce soit le but recherché par l'exercice.

Merci beaucoupppppppppppppppppppppppppppppppppppppppppppppppppp !