Bonjour

pour avoir la réponse, voir l'excellent film Las Vegas 21 !



sinon une petite discussion issue de ce film:

apres avoir lu tous les commentaires, je rajoute une petite précision: les 2/3 ne fonctionnent que si l'animateur propose systématiquement de changer apres avoir montré une/la  mauvaise porte! (ce qui semble être le cas dans ton énoncé)

en effet si cette option n'est offerte que parfois, on peut à l'extrême considérer le cas ou le présentateur ne fait cela que lorsque le candidat a choisi la bonne porte au départ; changer de choix devient alors un mauvais calcul dans 100% des cas.

(il faut donc  être un inconditionnel du superkado pour savoir si c'est le cas!)

bonjour il y a un chose qui me parait bizzare dans les réponses données pour ce genre d'exercice (juste pour en debattre)

au depart le candidat choisi parmi 3 boites celle qui devrait contenir le cadeau ( pas de soucis 1/3 de chance de tomber

sur la bonne boite ) ... ensuite l'animateur designe une boite vide et demande au candidat s'il veut modifier son choix

si le candidat sait donc que la boite designée par l'animateur est vide , il va forcement en faire abstraction pour

son prochain choix , s'il veut refaire un nouveau choix , ce sera donc entre la boite qu'il a deja choisie et celle qui

n'a pas été designée vide par l'animateur soit parmi deux boites et à ce moment là entre la boite deja choisie et celle

qu'il reste il devrait y avoir 1/2 de chance de tomber sur la bonne , la réponse de l'enoncé tient toujours compte de

l'existence de la boite vide designée par l'animateur d'ou les 2/3 de chances ... ca me parait un peu bizzare et pas tres

logique

Quand j'ai vu ce film il y a un certain temps deja, je m'etais dit que en fait ca ne changeait rien puisque quelle que soit la porte choisie au depart (donc avec une chance sur trois) bonne ou mauvaise l'animateur allait en designer une mauvaise et que au final meme s'il restait deux portes, on ne passait pas a une chance sur deux comme on essayait de nous le faire croire et que c'etait un leurre (en fait j'avais mal compris la reevaluation: je croyais qu'on passait d'une chance sur trois a une sur deux...), et qu'on avait bien qu'une chance sur trois.

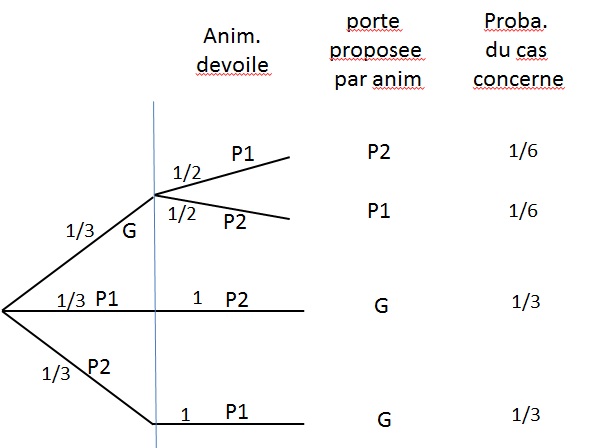
En fait c'est plus complique que ca, et si on fait un arbre en appelant G P1 et P2  les trois portes (gagnant perdant1 et perdant 2) bien evidemment indiscernables:

on verra que la porte G est proposee dans 2/3 des cas par l'animateur! (1/3+1/3)  et seulement dans 1/3 des cas(1/6+1/6), il propose une porte perdante.

Neanmoins quelques limites a cela:
1 il faut que l'animateur devoile systematiquement une porte perdante et propose de changer (sinon ca fausse completement, par exemple s'il ne propose de changer que quand la personne a designe la porte gagnante au depart!)
2 liee a la premiere, il faut que les candidats ne soient pas conscients de ces probas sinon ils changeraient a chaque fois et les animateurs finiraient par arreter de le proposer...