Inscription / Connexion Nouveau Sujet
Probabilité
Pouvez vous m'aidez s'il vous plaît,les proba c'est vraiment dure..😕
Un paquet contient 6 bonbons à la fraise et 10 au citron. On demande à Mathias de prendre au hasard l'un après l'autre deux bonbons dans le paquet. S'il tire deux bonbons de parfums différents, il a gagné le droit de les manger;sinon,il doit les remettres dans le paquet. On pense que ce jeu est équitable c'est à dire que l'on a autant de chances de gagner que de perdre. Pouvez vous confirmer cette affirmation?
Voila mon exercice, je sais qu'il faut faire un arbre mais je sais pas comment faire et faire la rédaction en expliquant mes calculs.
Bonjour,
pour le premier bonbon, quelle est la probabilité qu'il soit à la fraise ?
pour le second, quelle est la probabilité qu'il soit à la fraise aussi ?
fais pareil pour les bonbons au citron et déduis-en la probabilité pour que les deux bonbons soient les mêmes (en ajoutant les résultats que tu viens de trouver).
Pour mon arbre j'ai fais:
/6/16 fraise/5/15 fraise
\ 10/15 citron
\10/16 citron/ 6/15 fraise
\ 9/15citron
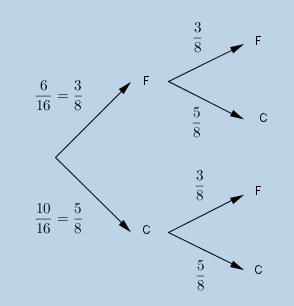
1 ere branche : 6/16 fraise
2 eme branche en dessous: 10/16citron
Les branches à coter:
1 ere: 5/15 fraise
2 eme: 10/15 citron
3 eme: 6/15 fraise
4 eme: 9/15 citron
Je suis nouvelle sur ce site je sais pas vraiment comment sa marche encore
et maintenant calcule les probabilités de fraise-fraise et citron-citron
(les probabilités se multiplient quand on parcourt l'arbre))
Il y a une erreur car au premier tirage il y a 16 bonbons dans le paquet, au second tirage il n'y en a plus que 15.
D'accord merci donc c'était bon ce que j'avais fait sauf que je simplifie et maintenant faut calculez les proba
ça dépend de ce que tu cherches à calculer.
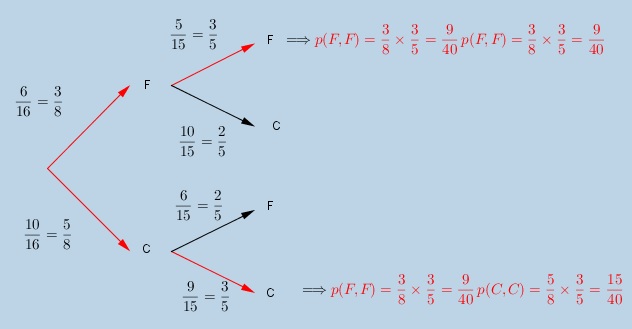
Pour ma part, j'ai regarder (en rouge) la probabilité d'avoir 2 parfums identiques.
(le 2ème rouge dans mon tableau est d'ailleurs p(C,C) et non pas p(F,F)
On pense que ce jeu est équitable c'est à dire que l'on a autant de chances de gagner que de perdre. Pouvez vous confirmer cette affirmation?
La question c'était ça
Il a une probabilité de 9/0 + 15/40 = 24/40 d'avoir 2 parfums identiques, et 24/40 ça ne fait pas 1/2
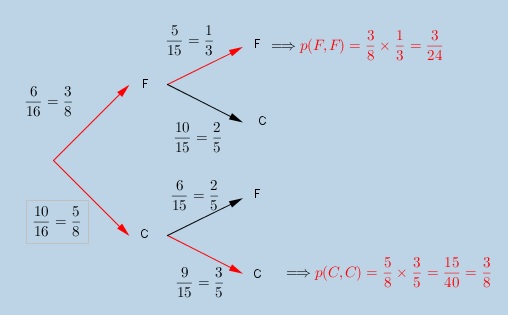
non, il y a une erreur Jedoniezh, c'est lui qui a raison.
l'erreur vient que 5/15 ne vaut pas 3/5 mais 1/3
et quand on calcule directement (6/16)(5/15)+(10/16)(9/15), on trouve bien 1/2