Inscription / Connexion Nouveau Sujet
Probabilité avec des arbres
Bonjour, ça fait un bon moment que je bloque sur cet exercice, sur comment faire l'arbre, et qu'est ce qui est vraiment demandé. Pourriez-vous m'aidez a résoudre ce problème
Deux objets P et T sont rangés de manière aléatoire dans trois caisses numérotées 1, 2, et 3
L'événement M est << la caisse n°2 est vide >>
1] On ne peut placer qu'un seul objet dans une même caisse. En utilisant un arbre, calculer la probabilité de M.
2] On peut placer les deux objets dans la même caisse. En utilisant un arbre, calculer la probabilité de M.
Merci d'avance 
Bonjour
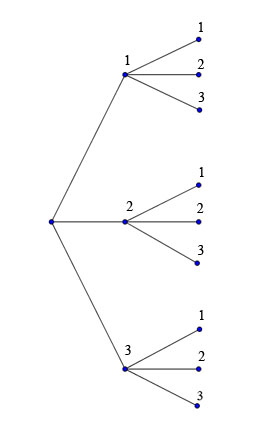
1)Je te propose cet arbre
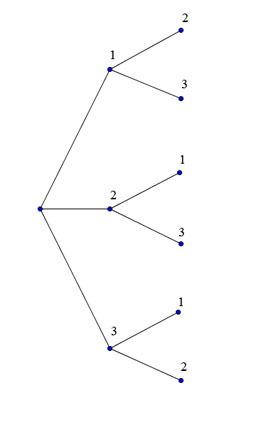
Un des objets est mis dans une des caisses, le 2ème dans une des caisses restantes
Ils sont rangés de manière aléatoire donc nous sommes dans une situation équiprobabilité.
Par conséquent...
2)
Merci c'est bien ce que je pensais pour les arbres, en revanche il est demandé de calculer la probabilité de M.
Si j'ai bien compris dans la question n°1 cela n'est pas possible , c'est ça ?
Et pour la question 2, comment fait-on pour calculer la proba de M ?
Si j'ai bien compris dans la question n°1 cela n'est pas possible , c'est ça ?
Si c'est possible.
Le 1er objet est mis dans une des caisses (1, 2 ou 3)
Le 2ème est mis dans une des 2 caisses restantes.
En regardant l'arbre, dans quel cas, aucun des objets n'est mis dans la caisse 2 ("la caisse 2 est vide")
Je suis désolée mais je ne comprends vraiment pas, ce que l'on doit calculer et comment on peut calculer car on n'a aucune donnée chiffrée
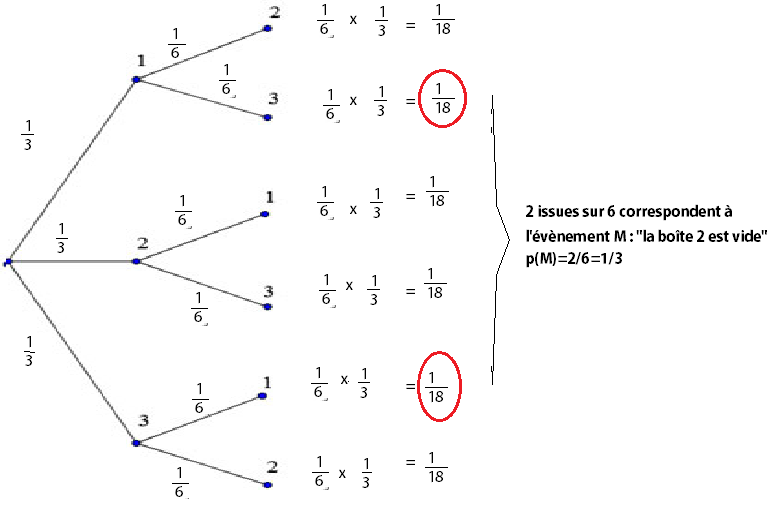
Bon, on reprend. Lis attentivement chaque ligne:
le 1er objet est dans la boîte 1, le 2ème est dans la boîte 2 ou 3
le 1er objet est dans la boîte 2, le 2ème est dans la boîte 1 ou 3
le 1er objet est dans la boîte 3, le 2ème est dans la boîte 1 ou 2
Au total, tu as 6 issues possibles.
Le rangement a été fait de manière aléatoire donc nous sommes dans une situation équiprobabilité.
Par conséquent, chaque issue a une probabilité de 1/6.
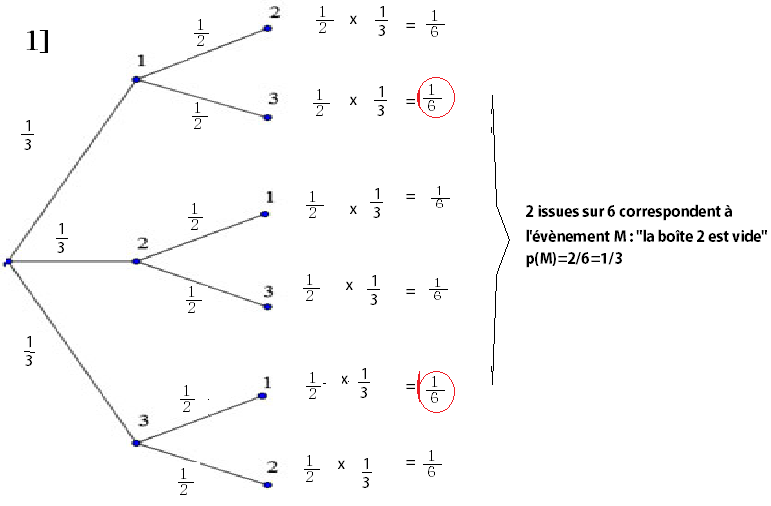
Dans quel cas, la boîte 2 est vide?:
le 1er objet est dans la boîte 1, le 2ème est dans la boîte 3
le 1er objet est dans la boîte 3, le 2ème est dans la boîte 1
2 issues sur 6 correspondent à l'évènement M : "la boîte 2 est vide"
p(M)=2/6=1/3
As-tu compris?
Je crois avoir compris des choses,
Pouvez me dire si de la cette façon c'est juste
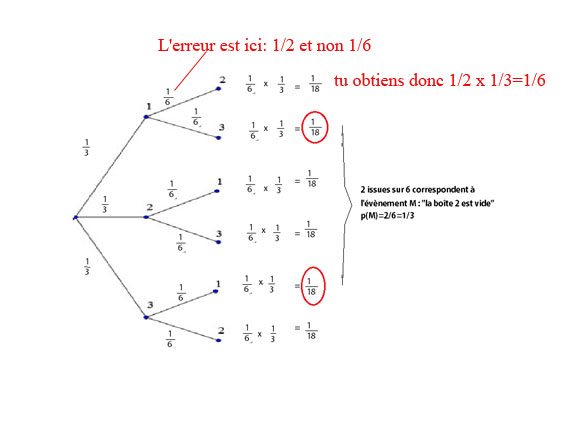
Je pense m'être trompée sur les calules
ah oui je suis bête !!! Merci
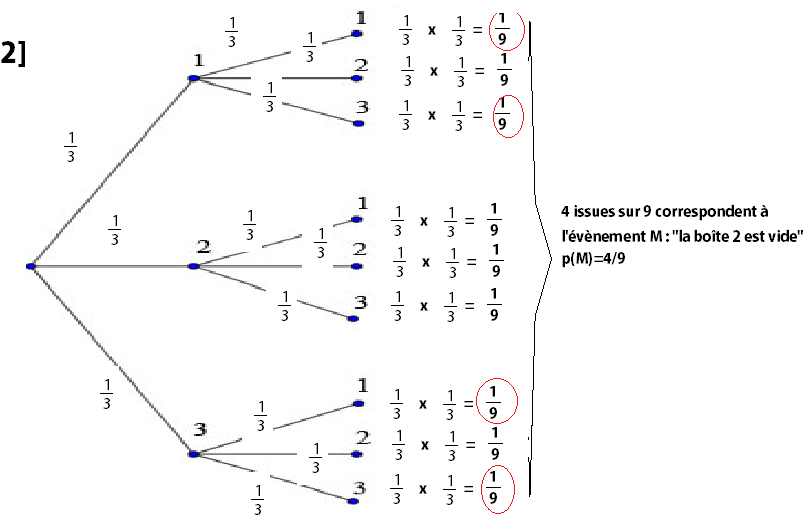
si j'ai bien compris les deux arbres devraient être juste
le n°1
le n°2
Est-ce juste ?