Inscription / Connexion Nouveau Sujet
Probabilité exercice niveau seconde
Une urne contient deux boules B1 et B2 et trois boules jaunes J1,J2 et J3, toutes indiscernables au toucher. On prend au hasard une boule, on note de quelle boule il s'agit, on la remet dans l'urne et on recommence une deuxième fois.
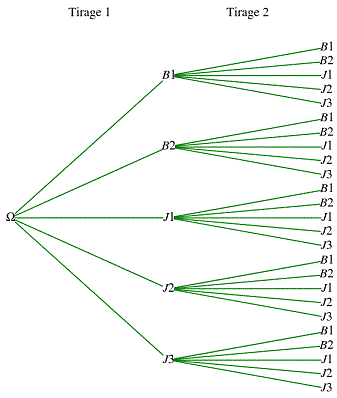
1) Donner l'arbre correspondant à la situation.
2) Déterminer la probabilité des événements suivants:
A :
Citation :
la première boule tirée est bleue et la deuxième est jaune
B :
Citation :
Les boules tirées sont de couleurs différente
C :
Citation :
Les boules portent le même numéro
3) Calculer la probabilité de l'événement B inter C
4)Calculer la probabilité de l'événement B union C
Merci d'avance pour l'aide que vous pourriez m"apporter
combien tu as d'issues sur ton arbre ?
quelle est la probabilité de tirer une boule bleue ?
une boule rouge ?
2) A : la première boule tirée est bleue et la deuxième est jaune
==> oui 6/25 c'est juste
2 façons de le trouver :
- soit on se sert de l'arbre, et on compte les issues qui correspondent : 6
- soit on multiplie les probas:
proba(tirer une bleue) * proba(tirer une jaune) = 2/5 * 3/5 = 6/25
euh
pour la c)
à la lecture des questions suivantes, il s'agit peut-être que du numéro, pas de la lettre
b) Les boules tirées sont de couleurs différentes
- soit on tire une bleue en premier puis une jaune : 2/5 * 3/5
- soit on tire une jaune en premier puis une bleue : 3/5 * 2/5
et on additionne : 6/25 + 6/25 = 12/25
l'arbre confirme ce calcul
on reprend la c), donc
Les boules portent le même numéro
on ne tient pas compte des couleurs, les numéros en question sont 1, 2 ou 3
Désolé, je n'ai pas compris la votre, laissez, donc pour la c) pouvez vous m'expliquez pourquoi 5/25 ?
pour la c) il faut comprendre la question ainsi :
Les boules portent le même numéro (soit1, soit2, soit3)
indépendamment de la couleur de la boule
les réponses 1/5 ou 5/25 ne conviennent donc pas,
car elles limitaient les possibilités à B1B1, B2B2, J1J1, J2J2 et J3J3
Donc pour récapituler
a) 6/25
b)12/25
c) 1/5 ou 5/25
ensuite pour le reste j'ai trouvé 13/125 est-ce sa? ( question 3) )
non, je t'ai expliqué que c) est fausse (relis mes posts)
3) B inter C
comment fais-tu pour trouver "sur 125" ?
il s'agit ici de l'événement :
"Les boules tirées sont de couleurs différentes ET elles portent le même numéro"
--- 2 conditions simultanées à remplir
c) par exemple
B1-J1 convient ---> les 2 boules portent le mm numéro
et
B1-B1 aussi
compte sur l'arbre toutes les possibilités
Il faut que je passe à un autre devoir de français et je n'ai plus de temps, je vais marqué ce que je pense et je verrais désolé.
4)Calculer la probabilité de l'événement B union C
c'est la réunion des 2 événements B et C
compte sur l'arbre les issues qui remplissent SOIT la condition B, soit la condition C, soit les deux en même temps.
3)
il s'agit ici de l'événement :
"Les boules tirées sont de couleurs différentes ET elles portent le même numéro"
--- 2 conditions simultanées à remplir
sans l'arbre, tu peux raisonner ainsi :
B1 ==> J1
B2 ==> ?
J1 ==> ?
J2 ==> ?
J3 ==> ?
a+
sa m'énerve car si je trouve la 3) j'ai la 4) car pour la 4 on fait p(A) + p(B) - p(AinterB) = p(AUB)