Inscription / Connexion Nouveau Sujet
Problème d'ellipse
Bonjour, voici l'énoncé d'un problème que je ne comprends pas... J'ai beau le lire et le relire, je ne sais pas faire de dessin. Pourriez-vous m'aider?
Un rayon lumineux issu du foyer F (-,0) de E
4x2 + 9y2 - 36 = 0 forme avec OI un angle dont la tangente est -2.
Déterminez une équation cartésienne de la trajectoire d du rayon réfléchi.
Bonjour,
Je suppose qu'on fait partir un rayon du foyer, et qu'il coupe l'ellipse E en I.
On considère alors l'angle (IF, IO), la tangente de l'angle (au sens "fonction tangente") doit être -2, ce qui permet de positionner le point I sur l'ellipse. Enfin on considère la tangente à l'ellipse en I (au sens "droite tangente"), on assimile cette tangente à un miroir sur lequel le rayon issu de F se réfléchit vers l'intérieur de l'ellipse, et c'est l'équation de ce rayon réfléchi qu'on cherche.
C'est vrai, et c'est d'autant plus curieux que l'exercice impose cette condition "un angle dont la tangente est -2" alors que c'est vrai pour tous les rayons issus de F...
C'est quoi I ?
a) Soit le point de l'ellipse où le rayon incident arrive sur l'ellipse
b) Soit le point de coordonnées (1 ; 0) comme souvent noté dans un système orthonormé.
---
Il va sans dire (mais cela va encore mieux en le disant) que suivant la réponse donnée à cette question, le problème est différent.

Voila des dessins (approximatifs) correspondant aux 2 cas que j'ai mentionnés
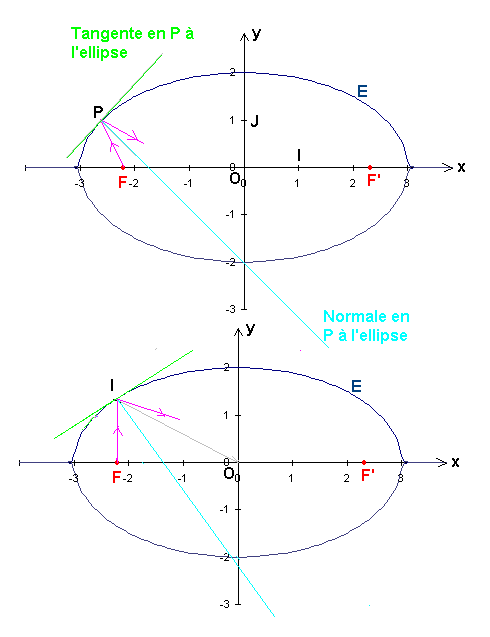
Lequel faut-il considérer ?

Bonjour et merci pour votre aide!
Je n'avais pas prêté plus attention à ce fameux point I et aux questions qui s'en suivent...
Après réflexion, je pense que ce serait bien le point de coordonnées (1,0).
Dans le premier dessin que j'avais essayé de faire, I était un point quelconque de l'ellipse par où le faisceau passait et c'était à partir de ce point qu'il était réfléchi.
Mais avec tes explications, il me semble plus logique que I serait bien le point (0,1) faisant partie de l'axe des abscisse vu qu'on parle de l'axe OI.
Oups, petite coquille..
Mais avec tes explications, il me semble plus logique que I serait bien le point (1,0) faisant partie de l'axe des abscisseS vu qu'on parle de l'axe OI.
Oubliez ce que j'ai écrit avant...
Je suis désolé, j'aurais dû me remettre complètement dans le problème...
Je confirme que le point I est bien le point (1,0). Parfois, on appelle l'axe des abscisses OI.
Le point qui touche l'ellipse, je l'avais appelé P (et non I comme je l'ai dit avant).
"Si mes souvenirs sont exacts, le rayon réfléchi passera toujours par l'autre foyer." Je n'en ai aucune idée.
A mon avis, le fait que la tangente soit égale à -2 devrait permettre de trouver le coefficient directeur du faisceau non?
Le faisceau émis aurait donc pour équation : y = -2x + k
Encore désolé pour le multi-post 
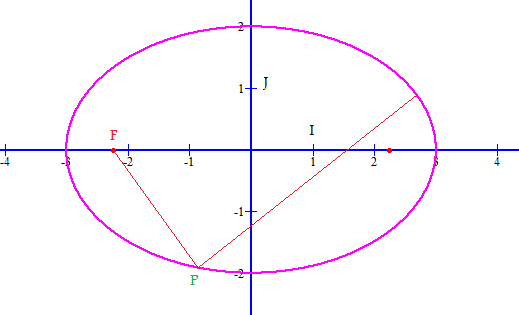
Rayon incident : y = -2x - 2V5
Les coordonnées de P se trouvent en résolvant le système :
4x²+9y²-36=0
y = -2x-2V5
Il y a 2 solutions, celle qui correspond à mon dessin de ma réponse précédente et celui de ton dessin.
Je retiens celle de ton dessin, on trouve : P(-0,6.V5 ; -0,8.V5)
Ellipse inférieure:
y = -(1/3)*V(36-4x²)
f(x) = -(1/3)*V(36-4x²)
f '(x) = (4/3).x/(V(36-4x²))
f '(-0,6V5) = -1/3
C'est la pente de la tangente à l'ellipse en P
La pente de la normale à l'ellipse en P est donc = 3
En appelant Q le point de rencontre de cette normale à l'ellipse en P et de l'axe OI, on a donc:
tg(OFP) = 2
tg(FQP) = 3
angle(FPQ) = Pi - angle(OFP) - angle(FQP) (la somme des angles du triangle FPQ égale Pi).
angle(FPQ) = Pi - arctg(2) - arctg(3)
angle(FPQ) = Pi/4
Et angle entre le rayon incident et le rayon réfléchi = 2 * angle(FPQ) = Pi/2 (soit un angle droit)
Angle entre axe OI et rayon réfléchi = Pi/2 - arctg(2)
tg(Angle entre axe OI et rayon réfléchi) = tg(Pi/2 - arctg(2)) = 1/2
Donc la pente du rayon réfléchi est 1/2
Le rayon réfléchi passe par P et donc son équation est :
y = (1/2)x - 0,5.V5
En y = 0, on a x = V5, ce rayon passe donc par le second foyer de l'ellipse.
-----
Sauf distraction. 
Merci J-P d'avoir confirmé par le calcul la propriété que je donnais plus haut.
Une application classique :
A Paris, les couloirs du métro ont une section transversale sensiblement elliptique. Si sur l'un des quais une personne parle (même doucement) en étant située approximativement à un foyer, toute personne située sur l'autre quai, également au voisinage de l'autre foyer, entendra la conversation.


