Inscription / Connexion Nouveau Sujet
Problème ouvert
Bonjour je dois réfléchir sur ce problème ouvert mais j'ai quelques difficultés :
Lors d'une loterie, chaque billet correspond à la tête, le corps ou les membres inférieurs d'un pantin. Un joueur gagne lorsqu'il parvient à constituer l'intégralité du pantin. Le règlement stipule que chacune des trois images est bien uniformément répartie sur l'ensemble des billets. Sur 1000 personnes ayant acheté un carnet de 10 billets, 49 n'ont pas gagné de lot. La distribution est elle bien uniforme ?
Je suis ouvert à toute aide et je vous en serai reconnaissant 
Bonjour,
Je pense qu'il ne faut calculer la probabilité de ne pas reconstituer le pantin avec 10 billets.
Et la comparer avec 49/1000
Nicolas
Ce n'est probablement pas ce qui est attendu, mais on peut essayer de simuler cette expérience informatiquement.
Ci-dessous un code en Processing (variante de Java).
Il simule 10 expériences comme celle proposée par l'énoncé.
Dix fois, il prend 1000 personnes, les fait jouer, et regarde combien n'ont gagné aucun lot.
Le résultat est le suivant :
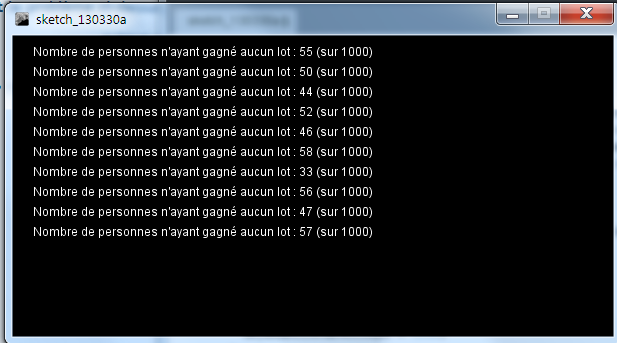
On voit que le résultat donné dans l'énoncé (49 personnes sont 1000 n'ont pas gagné le gros lot) est du même ordre de grandeur que les résultats obtenus informatiquement. Intéressant.
Ci-dessous le code, sous forme d'image, et en texte.
Tu peux le copier sur cette page : http://sketch.processing.org/
Puis cliquer sur la flèche en haut à gauche.
Le code va s'exécuter tout seul (sans rien installer), et la fenêtre de résultats va apparaître.
void setup() {
size(600, 300);
background(0); // fond noir
fill(255); // caractères blancs
noLoop();
}
void draw() {
for (int nbExperiences = 1; nbExperiences <= 10; nbExperiences++) {
int NbPersonnesAyantGagneUnLot = 0; // sera incrémenté à chaque fois que quelqu'un gagne un lot
for (int personneNumero = 1; personneNumero <= 1000; personneNumero++) {
int billetNumero = 1; // sera incrémenté à chaque billet examiné (jusqu'à 10)
boolean dejaUnBilletAvecTete = false;
boolean dejaUnBilletAvecCorps = false;
boolean dejaUnBilletAvecMembresInf = false;
while (billetNumero <= 10 && (! (dejaUnBilletAvecTete && dejaUnBilletAvecCorps && dejaUnBilletAvecMembresInf))) {
float reelAuHasard = random(1);
if (reelAuHasard < 1.0/3.0) {
dejaUnBilletAvecTete = true;
}
else if (reelAuHasard < 2.0/3.0) {
dejaUnBilletAvecCorps = true;
}
else {
dejaUnBilletAvecMembresInf = true;
}
billetNumero = billetNumero + 1;
}
if (dejaUnBilletAvecTete && dejaUnBilletAvecCorps && dejaUnBilletAvecMembresInf) {
NbPersonnesAyantGagneUnLot = NbPersonnesAyantGagneUnLot + 1;
}
}
text("Nombre de personnes n'ayant gagné aucun lot : "+(1000-NbPersonnesAyantGagneUnLot)+" (sur 1000)", 20, nbExperiences*20);
}
}

Ceci dit, je pense que ton professeur souhaite que tu calcules la valeur exacte de la probabilité. Est-elle proche de 49/1000 ?
On considère les 10 billets détenus par une personne.
On prend pour univers l'ensemble les issues élémentaires possibles, décrites par la succession des 10 billets.
En notant T, C et MI les trois types de billets possibles, une issue élémentaire est par exemple : T-T-MI-C-MI-T-T-T-C-C.
Cet univers est équiprobable.
On cherche à calculer la probabilité que la personne ne gagne pas de lot, de manière à la comparer avec 49/1000.
p = P("que des T et des C" ou "que des T et des MI" ou "que des C et des MI").
Les trois évènement sont disjoints, donc on peut écrire :
p = P("que des T et des C") + P("que des T et des MI") + P("que des C et des MI")
T, C et MI jouent le même rôle, donc :
p = 3*P("que des T et des C")
Reste à calculer P("que des T et des C").
En déduire p.
Puis comparer à 49/1000
Nicolas
On cherche à calculer la probabilité que la personne ne gagne pas de lot, de manière à la comparer avec 49/1000.
En examinant les différentes façons de ne pas être en mesure de reconstituer le pantin, on trouve que cette probabilité est égale à :
p = P("que des T et des C avec au moins un de chaque" ou "que des T et des MI avec au moins un de chaque" ou "que des C et des MI avec au moins un de chaque"...
... ou "que des T" ou "que des C" ou "que des MI").
Les six évènement sont disjoints, donc on peut écrire :
p = P("que des T et des C avec au moins un de chaque") + P("que des T et des MI avec au moins un de chaque") + P("que des C et des MI avec au moins un de chaque") + ...
... + P("que des T") + P("que des C") + P("que des MI")
T, C et MI jouent le même rôle, donc :
p = 3*P("que des T et des C avec au moins un de chaque") + 3*P("que des T")
Reste à calculer P("que des T et des C avec au moins un de chaque") et P("que des T")
En déduire p.
Puis comparer à 49/1000
Nicolas
1. Que vaut ?
Soit le nombre de "T".
peut varier de 1 à 9 (puisqu'on a au moins un "T" et au moins un "C")
Le nombre de "C" est
Le nombre de façons de placer les "T" (et donc les
"C") parmi les 10 billets est :
La probabilité d'avoir "T" et
"C" est
Finalement :
2. Quant à la seconde probabilité :
3. Finalement, la probabilité qu'une personne avec 10 billets ne puisse pas reconstituer le pantin, et donc ne gagne pas de lot, est :
4. L'énoncé indique que, parmi les 1000 participants, 49 n'ont rien gagné.
C'est une valeur "proche" des 52,58 théoriques.
Sans qu'on puisse en tirer une conclusion définitive, cela pousse à croire que la distribution des billets T, C et MI était effectivement uniforme.
Sauf erreur !
Nicolas
Merci beaucoup de ton aide et de ton investissement, grâce à toi j'ai compris et je t'en suis reconaissant ! 
( Une simulation de l'expérience en... LaTeX : https://www.ilemaths.net/sujet-programmer-et-faire-de-l-algorithmique-en-latex-549475.html )


