Inscription / Connexion Nouveau Sujet
Problème trigonométrie
Bonjour,
je n'arrive pas à répondre à quelques question de mon DM de maths, l'énoncé de l'énoncé de l'exercice est le suivant:
2) on considère l'expression suivante: A= (4n-7)²+26n-40+9n², où n est un entier.
a) Calculer A lorsque n=0,n=1,n=2, n=3: voici mes réponses: pour n=0: 9; n=1: 4; n=2: 49; n=3: 144
b)Démontrer que pour tout entier naturel n, A est un carré parfait: je dois simplement faire la racine carré de ces nombres et montrer qu'ils sont entiers ?
3)On considère dans le plan trois points A,B et C tels que: AB= √ 175; BC= √ 448; AC= √ 63
Ces trois points sont ils alignés ? Si oui, préciser dans quel ordre: cette question je ne sais pas y répondre (pour info la figure est en dessous...)
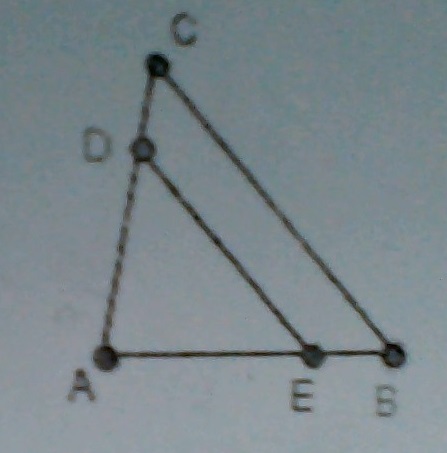
4) Dans le triangle ABC ci-contre, (échelle non respectée), on a:
(ED) est parallèle à (BC); AD= 3√ 2 -1; AB= 3-√ 2; AE= √ 2
Calculer DC. On donnera le résultat sous la forme a+b√ 2: cette question non plus je n'ai pas réussi...
5) On considère un triangle un triangle ABC tel que: AB= √ 3 - √ 2; BC= √ 6 +1; AE= 2√ 3
Ce triangle est-il rectangle ? Si oui préciser en quel sommet. : oui le triangle est rectangle par contre je ne sais pas quel est le sommet.
6)a. On considère le nombre suivant: A= √ 12+3√ 7 (la première racine continue jusqu'au bout)+ √ 12-3√ 7 (pareil)
Montrer que A² est un entier naturel. En déduire une écriture simplifiée de A après en avoir précisé le signe. : c'est un entier naturel car le résultat est 24, pour l'écriture simplifiée j'aurais dit: √ 24 ?
b) On considère le nombre suivant: B= √ 6-2√ 5 (première racine jusqu'au bout) - √ 6+2√ 5 (pareil)
Comparer √ 6-2√ 5 et √ 6+2√ 5. En déduire le signe B puis en procédant comme dans la question précédente, montrer que B est un entier relatif. : je n'ai pas trouvé non plus...
Merci d'avance
Bonjour,
2.b. On ne te demande de montrer que A est un carré parfait pour n=0, 1, 2 et 3, mais de montrer que c'est un carré parfait pour tout n.
Développons :
On reconnaît une identité remarquable :