Inscription / Connexion Nouveau Sujet
Produit scalaire
Bonjour,
Je n'arrive pas à résoudre la question 2.b., si quelqu'un peut m'aider.
Voici l'énoncé :
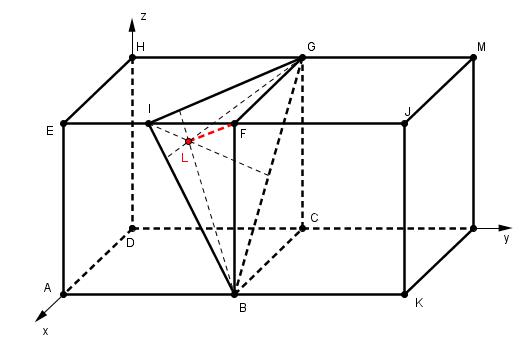
Deux cubes d'arête 1 sont disposés côte à côte. L'espace est rapporté au repère orthonormé (D;DA;DC;DH).
Le point I est le milieu de EF.
1.a. Démontrez que DJ est normal au plan (BIG).
b.Déduisez-en une équation cartésienne du plan (BIG).
2.a.Déterminez une représentation paramétrique de la droite D passant par F er perpendicualire au plan (BIG).
b.La droite D coupe le plan (BIG) en L. Le point L est-il l'orthocentre du triangle BIG ?
Je vous remercie.
Bonjour,
Comme nous on ne sait pas quels sont les points parmi les 12 sommets de cette figure qui s'appellent D, A, C et H ...
sans même parler de qui est E, F etc.
Le cube de gauche est le cube ABCDEFGH et le cube de droite BKLCFJMG.
En bas à gauche, on a le plan ABCD. En bas à droite le plan BKLC. En haut à gauche : EFGH et en haut à droite : FJMG.
Merci.
cela est plus clair avec une figure !
(pour savoir joindre une figure lire comprendre et appliquer la FAQ (un des boutons du haut)
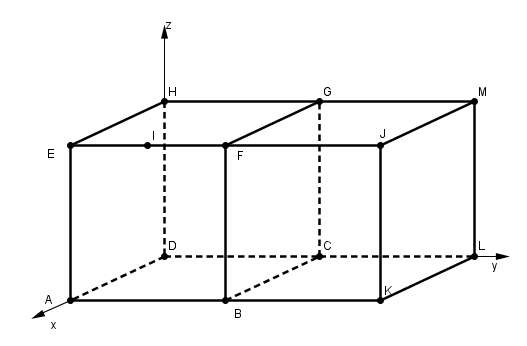
comme on te donne un repère, le faire avec des coordonnées est la "bonne" méthode
DJ est normal au plan (BIG) ssi est orthogonal à deux des vecteurs de ce plan, par exemple, à
et
donc : coordonnées des points, des vecteurs et produits scalaires.
ensuite pour trouver l'équation du plan, tu écris que pour tout point M (x; y; z) de ce plan, le vecteur est orthogonal à
(produit scalaire encore)
Bonjour,
J'ai fait les premières questions, mais c'est pour la questions : Le point L est-il l'orthocentre du triangle BIG ? , que je n'y arrive pas.
Merci encore pour votre aide.
2.b Tu pourrais déterminer les coordonnées du point L, puis regarder si la somme vectorielle LB + LG + LI est nulle ou non.
Tu as l'équation cartésienne du plan (BIG) et un représentation paramétrique de la droite (D).
Cela permet de déterminer la valeur du paramètre correspondant à leur point d'intersection.
Bonjour,
Si mes équations sont bonnes, je trouve L ( 1/4;5/4;1/4)
et LI+LB+LG = ( 5/4;-5/4;5/4) donc L n'est pas l'orthocentre. Est-ce normal ?
à mon avis tes coordonnées de L sont fausses ("5/4" est "visiblement faux" car L est à l'intérieur du cube ABCDEFGH)
et de plus ton critère pour "L est l'orthocentre" sur le vecteur LI+LB+LG ???
tu t'attends à quoi comme résultat de ce vecteur pour dire que c'est ou pas l'orthocentre ?
nota : il est l'orthocentre
c'est général pour tout tétraèdre comme FBGI de base BGI et avec FB, FG, FI orthogonales
le pied de la hauteur issue de F est l'orthocentre de la base.
nota : il y a un bug dans l'énoncé, il y a deux points L dans la figure
le sommet du cube de droite BKLCFJMG.
et la définition explicite d'un autre point L dans le texte :
la droite D passant par F et perpendiculaire au plan (BIG) coupe le plan (BIG) en L.
on va dire que le sommet en question du cube de droite ne porte pas de nom :
comme il ne sert à rien dans l'exo, on n'a pas besoin de parler de ce sommet là, donc de le nommer,
et que tu l'avais inventé pour décrire ce cube.
Bonjour,
Mon critère pour que L soit l'orthocentre est que la somme vectorielle LB + LG + LI soit nulle, et je ne la trouve pas égale à zéro.
Je vous donne ce que j'ai trouvé, pour que vous me puissiez me dire ce qui est faux :
équation de (BIG ) : x+2y+z-3=0
Représentation paramétrique de la droite D : x=-t+1
y=-t+2
z=-t+1
Est-ce juste ?
Je te remercie.
Je corrige mon erreur de 9h50 : la relation vectorielle que je t'indiquais concerne le centre de gravité du triangle BIG, et non son orthocentre. Donc, n'en tiens pas compte.
Je suis d'accord pour l'équation du plan (BIG), mais pas pour les équations de la droite (D).
Celle-ci a en effet la même direction (1; 2; 1) que la droite (DJ) et elle passe par le point F(1; 1; 1).
Bonjour,
pour l'orthocentre il suffit de prouver que les vecteurs et
sont orthogonaux, et
et
aussi.
prouvant que (BL) et (GL) sont deux hauteurs de ce triangle.
pour info (vu que le but de l'exo est de faire des calculs dans un repère !) la démonstration de la propriété générale que j'énonçais le 19-03-17 à 22:18
dans tout tétraèdre trirectangle SABC, (c'est à dire les angles en S sont droits) le pied de la hauteur SH est l'orthocentre de ABC
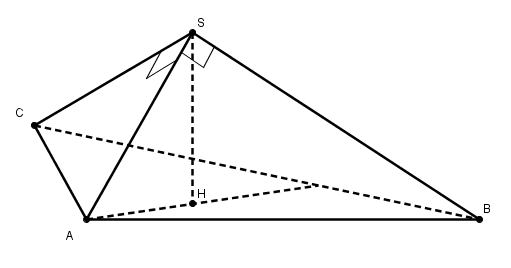
SA étant orthogonale à SC et SB, est orthogonale au plan SBC, donc à tout droite de ce plan, en particulier à BC
SH est orthogonale au plan ABC, donc à toute droite de ce plan en particulier à BC
BC est donc orthogonale à SH et à SA, donc au plan SAH
donc orthogonale à toute droite de ce plan, en particulier à AH
AH étant orthogonale (perpendiculaire) à BC est donc la hauteur de ABC
idem par permutations de ABC pour CH et BH
H est donc l'orthocentre de ABC.
ceci s'applique ici au tétraèdre FBGI de sommet F et les angles droits en F