re
ben ce sont tes conditions d'existence de l'équation qui t'imposent où tu as le droit de prendre tes points, oui ?

malou
faut il en parler lors de la conclusion ou considerer tout le cercle car le cercle englobe quelque parties qui ne verifient pas l equation la partie hachuree seule verifie toutes les conditions

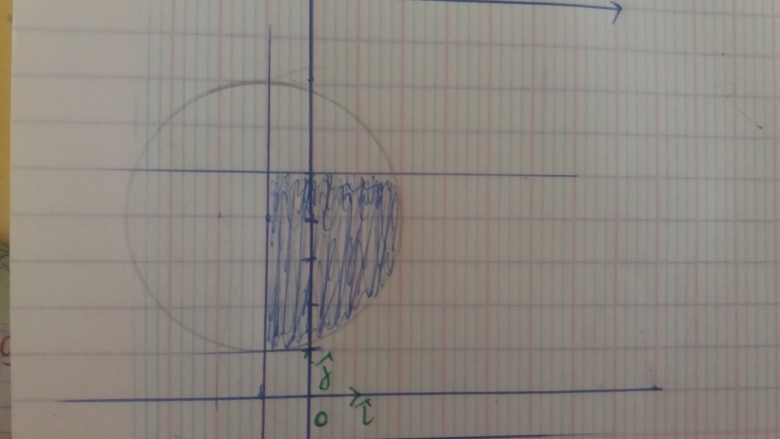
attention pour y
c'est entre -1 et 5
il y a quelque chose qui me choquait...tu as une erreur
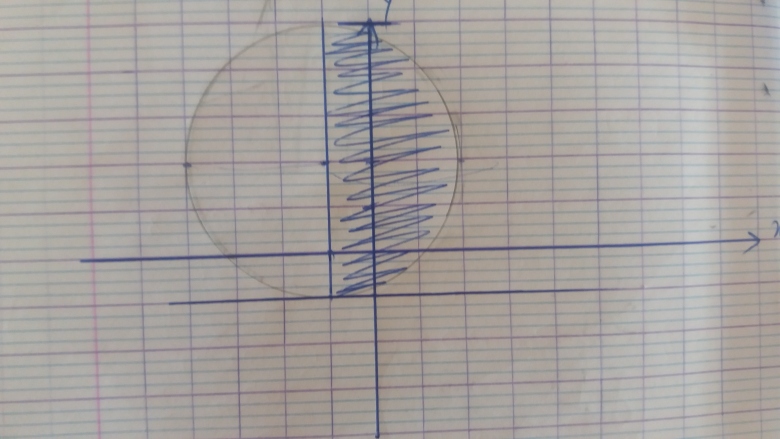
tu as une erreur pour ton centre
refais le...

oui oui c est enorme comme erreur
en fait la conclusion  va etre le demi disque de rayon 3 et de centre (-1;2)
est ce juste ?

eh oui !
tu diras bien si les extrémités du demi cercle sont prises ou pas

malou
oui je rectifie le disque fermé

euh c'est pas le disque
c'est le demi-cercle fermé

oui tu as raison malou
le disque on en parle lors des inequations
merci

salut

GKb @ 02-02-2020 à 13:56

determiner E tel que
E = {M(x;y)appartient au plan / x + 1 = (-y² + 4y + 5) }

l equation a un sens si et seulement si x>ou= -1 et y a [-1;5]

carpediem
salut
pardon mais le prof m a mis devant un dilemme
parfois il exige des conditions comme celle ci et parfois non
que dois je faire exactement s il vous plait

tu as une égalité qui pose un problème d'existence (ou de sens) :

pour comparer deux nombres ces deux nombres doivent exister (quelle est la différence entre un pigeon ?)

existe (toujours)

n'existe qu'à la condition que

une fois que ces deux nombres a et b existent alors il vient la question de leur égalité !!!

et évidemment l'équation a = b n'a pas de solution lorsque x < -1 de façon évidente ...

carpediem
oh merci beaucoup

de rien