Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Géometrie plane et dans l'espaceTopics traitant de Géometrie plane et dans l'espace [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Produit scalaire

Posté par
Milooser 19-01-21 à 14:12

Bonjour,
voici un problème donné par notre professeur.
On souhaite étudier les ensembles de points suivants:
Ek={M du plan tels que: MA2+MB2=k
Fm={M du plan tels que: MA2-MB2=m
Où k et m sont deux réel donnée et A et B deux point fixés.
1) A l'aide de Geogebra:
Créer un segment [AB] de longueur 10 (la longueur AB est automatiquement nommée a);
Créer un point M quelconque du plan, puis les segments [AM] et [BM].
Créer les longueurs AM et BM (automatiquement nommée b et c).
2)Dans le champ de saisie, entrer "k=b^2+c^2" puis valider.
a) Placer à présent M en A puis en B. Que  vaut k ? conjecturer la nature de l'ensemble E100 ; le tracer en vert
b)Placer M en I milieu de [AB]. Que vaut k ? Conjecturer la nature de l'ensemble E50.
c)Lorsque k vaut 0, comment se traduit la condition MA2+MB2=k et quel ensemble de points reconnaît -on  ?
3)Dans le champ de saisie, entrer "m=b^2-c^2" puis valider.
a) Lorsque k vaut 0, comment se traduit la condition MA2+MB2=k et quel ensemble de points reconnaît -on  ? Tracer en rouge l'ensemble F0.
b)Conjecturer en jouant sur la position de M la nature des ensembles F-120, F40, F100. Les tracer en rouge.
4) En introduisant le point I ,milieu de [AB], et utilisant un théorème bien connu, montrer que MA2-MB2=k<-> k/2-AB2/4.
5) Réécrire la condition MA2-MB2=m en transformant les carrés des longueurs en produits scalaire, puis en introduisant le point I, milieu de [AB], dans chacun des vecteurs, montrer que MA2-MB2=m<->AB.IM=1/2.
Utiliser un repère orthonormé judicieusement choisit pour obtenir un résultat permettant de décrire les ensembles Fm suivant la valeur du réel m.

1)J'ai réussi à faire le tracé sur geogebra.
2)a) k=100 et E100 est un cercle
b) k=50 , il est le centre du cercle et le milieu de [AB]
c) Il faut que MA et MB=0 Donc que  les points A,B,M soient confondues
3)a) Il faut que MA=MB. On reconnait les points du diamètre vertical de E100
b) C'est fait
4) J'ai essayé mais je ne comprend pas quelle théorème faut utiliser
5) je comprends rien du tout
Cordialement, merci d'avance.

Posté par
heklare : Produit scalaire 19-01-21 à 15:09

Bonjour

  1 joindre la figure
2 précisez le centre et le rayon
c k=0   les points A et B étant distincts  l'ensemble est vide

question 3 N'y aurait-il pas quelques confusions entre k et m ?

Posté par
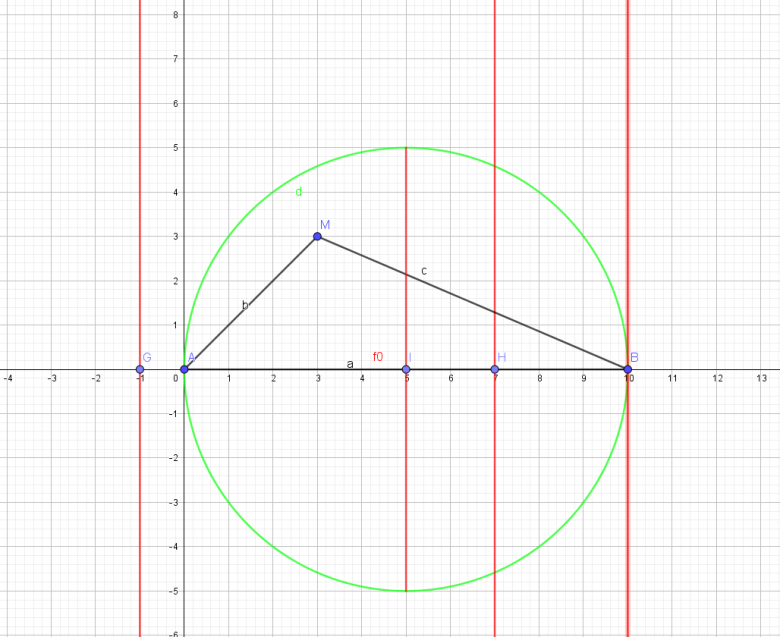
Milooserre : Produit scalaire 19-01-21 à 16:24

Bonjour,
merci de votre réponse. Pour la question numéro 3 il n'y a pas de confusion c'est bien cela. Et oui après vérification je vois que je me suis trompé  pour la 2. Voici ma figure.
Cordialement

Produit scalaire

Posté par
Milooserre : Produit scalaire 19-01-21 à 16:27

Milooser @ 19-01-2021 à 16:24

Bonjour,
merci de votre réponse. Pour la question numéro 3 il n'y a pas de confusion c'est bien cela. Et oui après vérification je vois que je me suis trompé  pour la 2. Voici ma figure.
Cordialement

Produit scalaire




Pour la figure la première droite  est F-120, la deuxième F0, la troisième  F40, la dernière F100 .
Cordialement

Posté par
mathafou Moderateurre : Produit scalaire 19-01-21 à 16:37

Bonjour,
la question 3a est ici une recopie à tort de la question 2b donc c'est faux.
que ce soit de ton fait ou une erreur de l'énoncé d'origine

3a correcte devrait être (il est absurde de poser deux fois une question identique !!) :

3)Dans le champ de saisie, entrer "m=b^2-c^2" puis valider.
a) Lorsque m vaut 0, comment se traduit la condition MA^2 moins MB^2=m et quel ensemble de points reconnaît -on ?
Tracer en rouge l'ensemble F0.

même genre de pataquès sur les questions suivantes :

4) En introduisant le point I ,milieu de [AB], et utilisant un théorème bien connu, montrer que MA2 plus MB2 = k<-> quoi = k/2-AB2/4.

5) Réécrire la condition MA2-MB2=m en transformant les carrés des longueurs en produits scalaire, puis en introduisant le point I, milieu de [AB], dans chacun des vecteurs, montrer que MA2-MB2=m<->AB.IM=1/2. et ça ne dépend pas de m ??


sur ce je vous laisse continuer avec hekla

Posté par
heklare : Produit scalaire 19-01-21 à 16:52

pour m=0 on a MA^2=MB^2 il n'y a pas de limite c'est toute la médiatrice de [AB]

faire bouger et M et voir ce qui se passe

Question 4  le texte à compléter est bien celui de mathafou  ( bonjour)

Posté par
Milooserre : Produit scalaire 20-01-21 à 11:23

Bonjour
merci de vos réponses. Vous avez toute à fait raison je mal recopié l'énoncé. Pour la question 3)a) c'est bien  MA2-MB2=m.
La question 4^: MA2+MB2 = k<-> MI2= k/2-AB2/4.
Et pour la question 5:  MA2-MB2=m<->AB.IM=m/2
Cordialement

Posté par
heklare : Produit scalaire 20-01-21 à 11:25

Que proposez-vous maintenant pour la question 4 ?

Posté par
Milooserre : Produit scalaire 20-01-21 à 12:03

hekla @ 20-01-2021 à 11:25

Que proposez-vous maintenant pour la question 4 ?
Pour la question 4, il faut utiliser le théorème de la médiane donc  d'après lui MA2+MB2=2MI2+1/2*AB2. Après il  faut isoler MI2. Cela est correct cependant la deuxième partie de la question (il vient  juste de l'ajouter) : Décrire alors les ensembles Ek  suivant la valeur du réel k. Cette question je ne comprends pas.
Cordialement

Posté par
heklare : Produit scalaire 20-01-21 à 12:20

MI^2=\dfrac{k}{2}-\dfrac{AB^2}{4}

A et B sont deux points donnés donc la distance AB est fixe. Par suite connaissant k,

\dfrac{k}{2}-\dfrac{AB^2}{4} est constant

d'où  l'ensemble des points M pour un k donné est  le \dots  de \dots I  et de \dots

Quelle condition pour k  ?

Posté par
Milooserre : Produit scalaire 20-01-21 à 13:21

hekla @ 20-01-2021 à 12:20

MI^2=\dfrac{k}{2}-\dfrac{AB^2}{4}

A et B sont deux points donnés donc la distance AB est fixe. Par suite connaissant k,

\dfrac{k}{2}-\dfrac{AB^2}{4} est constant

d'où  l'ensemble des points M pour un k donné est  le \dots  de \dots I  et de \dots

Quelle condition pour k  ?
La je sèche, je sais pas :?

Posté par
Milooserre : Produit scalaire 20-01-21 à 13:37

hekla @ 20-01-2021 à 12:20

MI^2=\dfrac{k}{2}-\dfrac{AB^2}{4}

A et B sont deux points donnés donc la distance AB est fixe. Par suite connaissant k,

\dfrac{k}{2}-\dfrac{AB^2}{4} est constant

d'où  l'ensemble des points M pour un k donné est  le \dots  de \dots I  et de \dots

Quelle condition pour k  ?
La condition pour k est de connaitre le carrée de MI et AB ?

Posté par
heklare : Produit scalaire 20-01-21 à 13:39

Ne citez pas  cela ne sert à rien sauf à alourdir

C'est pourtant ce que vous avez effectué dans la question 2

On prend AB=10 et k=100 donc IM^2=\dfrac{100}{2}-\dfrac{10^2}{4}=25

Vous aviez bien trouvé le cercle de centre I  et de rayon 5

Là on a une généralisation  puisque le texte ne précise pas la donnée de A et B ainsi que  la valeur de k.

Quelle doit être la condition sur k pour que \dfrac{k}{2}-\dfrac{AB^2}{4} puisse être considéré comme le rayon d'un cercle ?

Posté par
Milooserre : Produit scalaire 20-01-21 à 14:02

Il faut que  K =10 et IM= 5 ?

Posté par
Milooserre : Produit scalaire 20-01-21 à 14:07

je voulais dire plutôt que K=100 et IM=5

Posté par
heklare : Produit scalaire 20-01-21 à 14:07

Non
\dfrac{k}{2}-\dfrac{AB^2}{4}\geqslant 0 \iff k \geqslant \dfrac{AB^2}{2}

dans la question 2 on avait bien le cercle car 100\geqslant 50 mais si vous cherchiez pour k=50 alors le cercle était réduit à un point


Rechercher
Menu
Espace membre
41 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1719 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !