Inscription / Connexion Nouveau Sujet
Produit scalaire
Bonsoir à tous j'ai un exercice de produit scalaire que je n'arrive pas à traiter
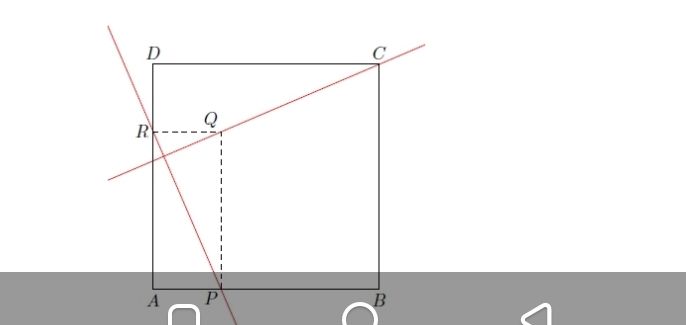
Soit un carré ABCD. On construit un rectangle APQR tel que :
- P et R sont sur les côtés [AB] et [AD] du carré ;
- AP = DR.Le problème a pour objet de montrer que les droites (CQ) et (PR) sont perpendiculaires.
1. Justifier que : CQ.PR=CQ.(AR-AP)
2. En déduire que les droites (CQ) et (PR) sont perpendiculaires
J'ai réussi à faire la première question mais la deuxième là je trouve pas si vous pouvez m'aider merci d'avance
salut
donc tu n'as pas fait grand chose :...
1/ est juste la relation de Chasles ...
2/ peut-être développer le produit scalaire de 1/ et utiliser le fait que dans un rectangle il y a plein d'angles droits ... en décomposant le vecteur CQ à l'aide de la relation de Chasles lui aussi ...
2/ peut-être développer le produit scalaire de 1/ et utiliser le fait que dans un rectangle il y a plein d'angles droits ... en décomposant le vecteur CQ à l'aide de la relation de Chasles lui aussi ...
mais vu la figure cette décomposition est inutile !!!
comment as-tu fait avec le vecteur PR ?
C'est selon la première question que j'ai décomposé le vecteur PR dans la question 1 on demande de démontrer que CQ.PR= CQ.(AR-AP) j'ai fait de la manière suivante CQ.PR=CQ.(PA+AR)=CQ.(-AP+AR)=CQ.(AR-AP).
ok ... tu as donc décomposé PR en deux vecteurs orthogonaux ...
que sais-tu sur le produit scalaire ?
donc en réfléchissant sur les propriétés du produit scalaire comment décomposer CQ le plus judicieusement ?
J'ai développé le produit scalaire CQ.(AR-AP)=CQ.AR-CQ.AP
J'ai calculé séparémment les deux produits scalaires avec le théorème de la projection (voir cours)
En projetant sur (AD) :
CQ.AR=DR.AR
Ces vecteurs étant de sens contraire :
CQ.AR=−DR×AR
En projetant sur (AB) :
CQ.AP=BP.AP
Ces vecteurs étant de sens contraire :
CQ.AP=−BP×AP
D'où :
CQ.PR=(−DR×AR)+(BP×AP)
Et on conclure
ok ... tu as donc décomposé PR en deux vecteurs orthogonaux ...
que sais-tu sur le produit scalaire ?
donc en réfléchissant sur les propriétés du produit scalaire comment décomposer CQ le plus judicieusement ?
donc on a tout simplement
PR = PA + AR
CQ = CD + DR + RQ
et on calcule le produit scalaire (PA + AR).(CD + DR + RQ) ...


