- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Ensemble et application Partie II
- Un best-of d'exos de probabilités (après le bac)
- Espaces vectoriels et Applications linéaires - supérieur
Inscription / Connexion Nouveau Sujet
Produit tensoriel
Bonjour,
Dans le cadre de l'approximation des EDP par éléments finis, on considère le produit tensoriel de fonctions, mais je ne sais pas du tout ce que c'est, et mes recherches sur internet n'ont rien données.
En gros, pour expliquer brièvement, on a Q1 l'espace vectoriel des polynomes de degré inférieur ou égal à 1 par rapport à chacune des variables x1 et x2.
On définit 4 polynomes qui sont dans Q1:
etc...
Et on a que les sont exactement les produit tensoriels des fonctions de base
et
sur le segment [0,1] où
et
Voilà, je sais pas si c'est clair, mais en gros je capte pas trop ce que c'est le produit tensoriel, et j'en ai besoin pour la suite du cours 
Merci d'avance 
Bonjour,
prends le vecteur ligne U = (x1 x2) et le vecteur colonne V = ( (1-x1) ; (1-x2) )
Si tu calcules le produit UV, tu obtiens une matrice 2*2 dont les composantes sont les 4 fonctions p1, p2, p3 et p4
Salut Jamo,
Je comprends pas trop, si je fais le produit matriciel de ces 2 vecteurs, j'obtiens une matrice à un seul élément, non ?
C'est ce qui m'est venu à l'esprit quand tu as parlé de produit tensoriel ... (un tenseur, c'est plus ou moins une matrice)
Bonjour à tous
on peut aussi parler de produit tensoriel de fonctions sans passer par les matrices.
En effet, si f et g sont deux fonctions à valeurs réelles (ou complexes) alors on définit le produit tensoriel de f et g, et on note par la formule
.
Sinon, Rouliane, tu trouvais cette opération tordue : eh ben t'as rien vu parce que c'est pire que ça. Le produit tensoriel est truc encore plus général et c'est moche !!  (un truc d'algèbre quoi !!
(un truc d'algèbre quoi !!  )
)
Kaiser
Merci !
Bon ben je vais pas etre décu si c'est encore plus tordu que ça 
En lisant un peu la suite, on retrouve bien ce que tu dis Kaiser, à savoir un produit f(x)g(y) mais c'est mal expliqué dans le bouquin...
Bon ben je vais pas etre décu si c'est encore plus tordu que ça



Disons que dans le cas général, le produit tensoriel est un peu difficile à se représenter et à manipuler.
Si un jour, tu te mettais à étudier les modules (qui, apparemment, sont au programme de l'agreg, du moins, les bases disons), tu risques de rencontrer du produit tensoriel.
En lisant un peu la suite, on retrouve bien ce que tu dis Kaiser, à savoir un produit f(x)g(y) mais c'est mal expliqué dans le bouquin...
OK !
Kaiser
Il me semble avoir lu rapidement dans un livre qu'on utilisait aussi le produit tensoriel dans les distributions ( avec la convolution je crois )
Exact ! on définit, dans certaines conditions, la convolution de 2 distributions à partir du produit tensoriel de 2 distributions (ça par contre, je ne sais pas si tu l'as déjà rencontrée cette dernière opération)
Kaiser
Non j'ai jamais vu cette formule, je me suis d'ailleurs arrété à la convolution parce que ça me servira apparemment pas pour cette année  ( ouf ! )
( ouf ! )
Pour revenir à la question initiale sur le produit tensoriel de fonctions, tu auras peut-être déjà rencontré la notation où E désigne par exemple, l'ensemble des fonctions continues sur [0,1] à valeurs complexes.
Avec cette notation, on serait tenté de dire que c'est l'ensemble des fonctions de la forme où f et g sont dans E mais ce n'est pas ça.
En fait, c'est l'ensemble des fonctions qui s'écrivent comme une somme finie de fonctions de cette forme.
Du coup c'est un espace vectoriel et on a même
Puisque j'en ai parlé, autant aller jusqu'au bout ! 
Pour la culture :
Cet espace vectoriel est un sous-espace dense de l'ensemble des fonctions continues sur [0,1]², pour la norme uniforme.
Cela découle du théorème de Stone-Weierstrass.
Kaiser
un truc d'algèbre quoi !!
Je m'absente 2 jours et on lit de ces choses (entre toi et J-P
 )
)
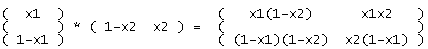



 autre en post-bac
autre en post-bac