Inscription / Connexion Nouveau Sujet
Produits scalaire , équations, transformation rotation
Bonjour
On donne E={M(x,y)/x²+y²-2xy-2x-2y+1=0}
f: P-->P
M--->M'(x',y')/ x'=√2/2(x-y) et y'=√2/2(x+y)
A) calculer OM, OM', mes(OM,OM') puis en déduire la nature de f
B) déterminer f(E)
C) Étudier F=f(E) . Construire F puis E
Donc j'ai fait A et B
OM=OM'=√(x²+y²) , mes(OM,OM')=45° on déduit que f est rotation r(O, 45°)
f(E)= 2y² -2x√2+1=0
Je suis bloqué au niveau de C besoin d'aide
salut
si tu exprimes x en fonction de y qu'obtiens-tu (tout simplement) ?
mais es-tu sûr de ton résultat pour f(E) ?
Pour le f(E)={M'(x',y')/x'²+y'²-2x'y'-2x'-2y'+1=0}
Puis j'ai remplacé. J'ai vérifié mais ça donne toujours ça
x en fonction de y
x=(2y²+1)/2√2
Peux tu expliquer parceque je ne vois pas
Bonjour
en l'absence de carpediem
il faut dans l'équation de E remplacer et
en fonction de
et
on veut une relation entre les coordonnées de M'
J'ai fait ça ici
f(E)={M'(x',y')/x'²+y'²-2x'y'-2x'-2y'+1=0
Ensuite je suis revenue avec les x et y et ça me donne
f(E)= 2y² -2x√2+1=0
Ce que vous faites là,
Vous cherchez l'ensemble des points M pour que l'image soit l'ensemble E
Ce n'est pas ce que l'on veut
de
écrivez les valeurs de x et y en fonction de x' et y' et remplacez dans l'équation de E
D'accord
Écrivez cette relation différemment, vous reconnaîtrez l'équation d'une courbe connue.
Vous pourrez alors dire que F est une conique ayant telles particularités
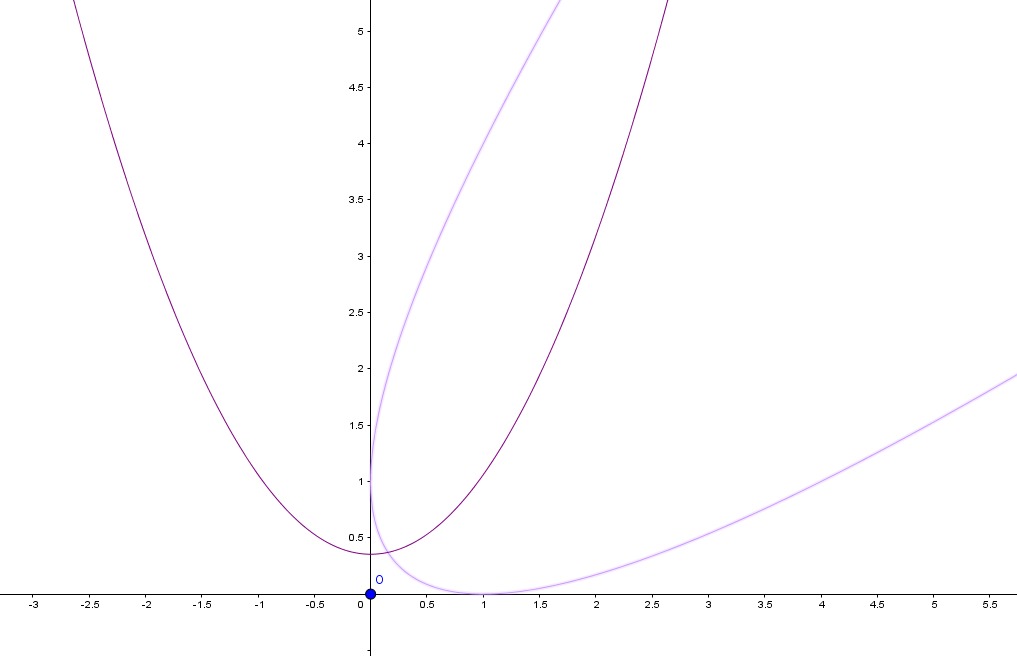
Si vous connaissez GeoGebra utilisez-le
Vous demandez la construction de E et vous appliquez ensuite la rotation
Ce qui est le sens contraire de la question, sens normal, car il est plus facile de tracer F que E sauf à la tracer point par point
Précisez ce qui permettra de savoir comment elle est tournée
Je ne pense pas que vous sachiez définir une parabole comme ensemble de points équidistants d'un point et d'une droite