Inscription / Connexion Nouveau Sujet
pythagore
Bonjour,
Quelqu'un peut-il m'aider s'il vous plait, j'ai un exercice de math et je ne sais pas comment m'y prendre. Voici l'énoncé
antonia,claudia et le petit romain s'amusent beaucoup dans le verger de Pépé José.le jeu consiste à rejoindre le plus rapidement possible le cerisier en partant d l'abricotier et en touchant le mur.
1.pour augmenter les chances de gagner le jeu,il faudra que le chemin de la course soit le moin long posssible.
a quelle distance du point H peut-on penser qu'il faudra toucher le mur pour que le chemin soit le moins long possible?
faire une figure à l'echelle dans ce cas et calculer la longueur du chemin.
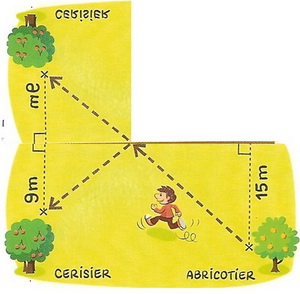
2.le petit romain a une idée génial:il trace le symétrique de cerisier par rapport au mur.
expliquer pourquoi le chemin de la course le moins long possible est égal à la distance séparant l'abricotier du symétrique du cerisier.
3.calculer la longueur séparant l'abricotier du symétrique de cerisier et en deduire la longueur de chemin le plus court possible.
comparer ce resultat à celui conjecturé dans la question 1.
A mon avis il faut que j'utilise le théorème de Pythagore.
S'il vous plait aider moi
Merci à ceux veulent bien m'aider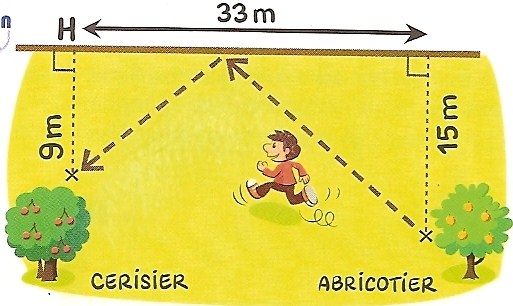
édit Océane : forum modifié
Bonjour vie
Je vois dans ton profil que tu es en seconde. Cela paraît plus logique pour un tel problème.
Si nous notons les points C pour le cerisier, A pour l'abricotier et P pour le point de rencontre avec le mur et Q pour le point du mur situé à 15 m de l'abricotier, alors les triangles CHP et AQP sont semblables.
On a donc : .
Si HP = x, alors PQ = HQ - HP = 33 - x.
Dès lors : .
Tu peux alors trouver x.
Pour la question 2, au vu du dessin, on voit directement que le chemin le plus court entre deux points est la ligne droite.
Il faut donc utiliser la symétrie pour montrer que cette ligne droite est la longueur demandée.
Bonjour,
merci pour votre réponse.
En fait ça n'est pas un exercice de seconde c'est pour mon frère qui est en 4ème
Je suis entrain d'esssayer de comprendre mais je n'y comprend pas grand chose.
Qand j'ai écrit
alors les triangles CHP et AQP sont semblables.

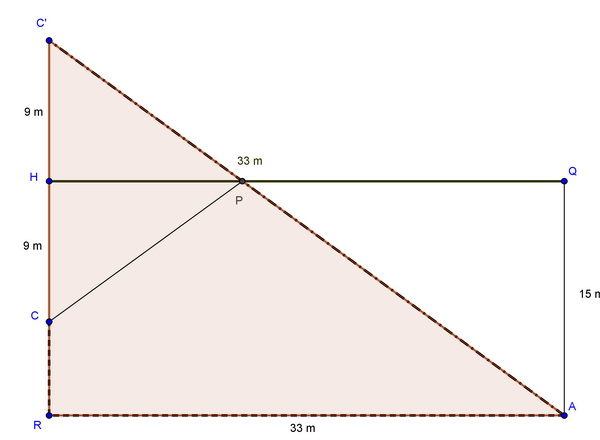
Voici d'ailleurs une figure qui reprend tout l'énoncé et qui permet de trouver la longueur cherchée.
Bonjour,
Pour calculer x dans la question 1
j'ai fait
x multiplié par 15 = 33 -x multiplié par 9
après j'ai un doute pour isoler le x.
Quelqu'un peut-il m'aider s'il vous plait.
Merci
Merci pour ta réponse.
En fait moi j'étais bloqué car je ne sais pas pourquoi mais j'avais passé le 15 tout de suite de l'autre côté et je ne savais plus comment procédé pour trouver le x.
Merci beaucoup de ton aide.
Bonjour,
Je suis un peu embêtée avec ce problème. Ma cousine a cet exercice à faire pour la rentrée. Elle n'est qu'en 4ème et votre méthode me paraît difficile vu son niveau. Elle ne comprend pas d'où vient ces rapports égaux. N'y-a-t-il pas une méthode plus simple pour trouver HP?
S'il vous plait, éclairez ma lanterne?
En attendant merci
Bonjour hatide,
Pour répondre à ta question, il y a deux démarches.
1) Elle est écrite dans l'énoncé :
faire une figure à l'echelle dans ce cas et calculer la longueur du chemin.
2) La valeur exacte pourra ensuite être calculée par Pythagore dans le triangle rectangle ARC'.
La distance cherchée est l'hypoténuse AC'.
Les deux côtés de l'angle droit ont comme mesures : AR = 33 et RC' = RH+HC' = 15+9 = 24.
Merci beaucoup Hiphigénie pour tes précieux conseils!
Cela me semble plus clair! Je n'avais qu'à lire mieux l'énoncé pour la question 1.
Pour la question 2, c'est ce que j'avais trouvé.
Je n'ai plus qu'à refaire l'exercice et l'expliquer à ma cousine.
Encore une fois, merci beaucoup et bonne soirée!
Je te remerci infiniment hiphigenie car grâce à toi j'ai compris cet exercice il me parrait un peu dur pour un 4eme car mon prof remplaçant est nul je suis passé de 19 de moyenne en maths a 12 de moyenne. Donc je te remercie grâce à toi j aurais une bonne note a mon DM.
Par contre je croyais avoir trouvé mais non car je ne comprends pas comment trouver la longueur AP et la longueur CP aidez moi s'il vous plait
Pourquoi veux-tu calculer ces longueurs ?
Relis les premiers messages.
En fait, il faut calculer la longueur AC', ce qui est très simple...
--Bonjour,
la réponse à la question 1 se base sur l'hypothèse que les triangles doivent êtres semblables afin que le chemin soit le plus court. Pourquoi une telle affirmation ?
Sous une autre formulation:
Si les triangles sont semblables alors le chemin est le plus court, pourquoi ?
Merci --
Bonjour mslider,
Ce topic pose problème car il a été posté par un membre du niveau seconde.
Il est donc classé dans la catégorie "seconde" et la solution que tu peux lire conviendrait bien pour un(e) élève de seconde.
Il s'est avéré ensuite qu'il était posé pour quelqu'un du niveau quatrième.
Je vois que ton profil te situe en troisième.
Il y a de quoi y perdre son latin... 
Alors, voici des indications pour le niveau "quatrième" où il ne sera plus question de triangles semblables.
La première question demande d'estimer à quelle distance du point H il faudrait toucher le mur pour que le chemin soit le moins long possible.
Il faut donc que tu donnes ce qu'intuitivement tu crois être la bonne distance.
L'énoncé demande ensuite de faire une figure à l'échelle avec la distance que tu as choisie et ensuite de calculer la longueur du chemin.
Donc plus question de triangles semblables, mais d'un simple calcul basé sur un dessin à l'échelle.
--Certes,
mais outre les différents niveaux d'études (4ième, 3ième, seconde..),
quand est-il de la vraie solution mathématique à ce problème ?
Une étude de fonction permettrait de trouver HP(x), mais existe t-il une solution plus simple ?
Merci --
Bonjour,
la solution simple est donnée dans l'énoncé : c'est les questions 2 et 3
on peut même la généraliser ad libitum :
si on doit passer par les deux murs

B' le symétrique de B par rapport au mur 2, B'' le symétrique de ce point B' par rapport au mur 1
par symétries le trajet A - C - D - B (quelconque) est de même longueur que le trajet A - C - D'' - B''
et est plus long que le trajet A - Cm - D''m - B'' (la ligne droite est le plus court chemin)
d'où le trajet le plus court en rouge
obtenu en "visant" à chaque fois l'image de B par ces symétries
(imaginer que les deux murs seraient des miroirs)
nota : si le segment AB'' ne coupe pas le mur 1, il coupe forcément alors le mur 2 et le trajet le plus court sera alors un trajet A - mur2 - mur1 - B
--
Oui, cette explication avec les 2 murs complique un plus le problème.
Sans utiliser les questions 2 et 3, peut-on répondre à la question 1 en démontrant que les triangles sont semblables et si oui comment démontrer qu'ils le sont ?
Merci --
la question 1 il n'y a aucun triangle semblable ni rien
c'est juste du "feeling" et rien d'autre en traçant un trajet "au pif" que l'on pense être peut-être suffisamment court comme ça.
Hiphigenie a eu parfaitement tort de partir directement là dessus
parce que ces triangles semblables n'apparaissent que une fois qu'on a fait la question 2-3 et résolu le problème pas avant
alors certes la solution étant bien connue (archi-classique) on peut exhiber ces triangles semblables parce qu'on connait déja cette solution (les questions 2-3) et uniquement pour ça. et ça n'a rien à faire question 1.
--
Très bien. C'est très clair maintenant.
Pauvres élèves de 4ième, car ce problème apparait bien dans le livre de mathématiques
de 4ième.
L'étude de fonction reste une solution sure pour résoudre la première question sans tenir compte du reste du problème.
je vais me répéter au risque de paraitre radoter :
la question 1 ... c'est juste du "feeling" et rien d'autre en traçant un trajet "au pif" que l'on pense être peut-être suffisamment court comme ça.
et l'on calcule la longueur de ce trajet choisi par deux fois Pythagore et c'est tout
rien d'autre
par exemple moi je dis que je pense que le trajet le plus court à mon avis serait de toucher le mur en un point B à 9m de H (pourquoi pas, c'est un trajet au pif, et c'est ce qu'on demande dans cette question 1, RIEN de plus !!)
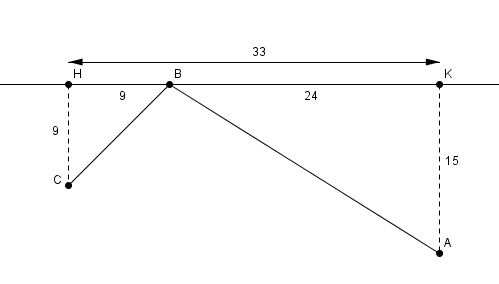
alors de A à B Pythagore me dit
de B à C
et donc mon trajet total ≈ 28.3 + 12.7 = 41m
point barre fin de la question 1.
(chacun choisit librement le point C là où il pense que ça serait selon lui un candidat raisonnable et rien d'autre)
et il faut arrêter d'inventer dans un problème de 4ème des questions de niveau première, voire Terminale (étude de fonction) qui n'y sont absolument pas du tout
et d'interpréter de travers ce qui est écrit à la lettre dans l'énoncé en comprenant autre chose que ce qui est demandé.
par exemple que l'on demanderait de calculer la position optimale de B (au plus simple niveau 3ème, question 4 avec Thalès papillon, pas demandée)
--
A aucun moment dans la question 1 il est précisé de répondre à l'intuition !
Et quand bien même si tel était le cas, bon nombre d'élèves et de personnes sur la planète iraient toucher le mur en son milieu, ce qui est très loin d'être la solution voir s'en approcher.
Si! Quand on lit ça:
a quelle distance du point H peut-on penser qu'il faudra toucher le mur ...
C'est de l'intuition qui est attendue.
Confirmation en fin de question 3:
comparer ce resultat à celui conjecturé dans la question 1
Va pour l'intuition.
Désolé mais j'ai pas appris à répondre à l'intuition dans un problème de Mathématiques.
De mon temps ce genre de question n'aurait pas eu lieu d'être, peut-être aussi que les
les mathématiques étaient considérées comme une science exacte.
Dans le même style on pourrait imaginer une question 1bis: même question qu'en 1 mais cette fois les yeux bandés.
n'importe quoi.
il ne s'agit pas d'intuition du tout mais d'initiative, de choisir un point arbitraire
(et d'ailleurs celui que j'ai choisi n'a rien à voir avec le vrai point optimal qui est à 12.375 de H comme le montrerait la question "4" pas demandée !!
faut bien lire les questions telles qu'elles sont demandées
des réponses pas lues entre temps
bon nombre d'élèves et de personnes sur la planète iraient toucher le mur en son milieu,
eh bien qu'ils le fassent et ça répondra à la question 1 telle qu'elle est demandée !!
point barre.
Et puis c'est formateur de se faire une idée de la réponse à apporter. Conjecturer quoi.
Puis de vérifier si la conjecture était judicieuse ou pas.
Dans certains métier, on appelle ça "pédagogie de la découverte".
Ça a bien sûr des limites.
et puis toute cette discussion surréaliste est sur le fait de savoir lire correctement un énoncé et de ne pas imaginer que on doit résoudre le problème (trouver réellement le vrai optimum) avant même d'avoir terminé l'exo !!
vu que le but de l'exo est justement d'arriver à la fin de l'exo, à le trouver, cet optimum !
et encore, vu qu'ici il n'est même pas demandé !!
ne pas confondre le but général de l'exo avec les questions effectivement posées telles qu'elles sont posées.
1. à quelle distance du point H peut-on penser qu'il faudra toucher le mur pour que le chemin soit le moins long possible?
si un élève pense que c'est au milieu, et bien il n'a pas d'autre choix que de dire "je pense que c'est au milieu" et de faire le calcul correspondant à ce point là
et si un autre élève pense que c'est à une distance de H égale à la plus petite des deux distances = 9, et bien il le dit et fait les calculs correspondant à ce point là
etc etc
chacun pense ce qu'il veut et on demande juste ce qu'il pense, honnêtement, comme c'est explicitement demandé dans l'énoncé.
et c'est ce défaut (croire qu'on en demande plus que ce qu'on demande vraiment) qui bloque de nombreux demandeurs ici : comprendre les énoncés de travers.
dans ce cas on peut aussi répondre le point Q qui est à 33m du point H. En gros répondre n'importe quoi entre H et Q. Et comme çà tous le monde gagne à la question 1.
Je vais dire à mon ami maçon d'oublier Pythagore et de construire ses murs à l'intuition.
Moi les conjectures je les laisse aux philosophes.
et bien ya qu'à mieux écrire les énoncés, çà éviterait aux élèves d'ouvrir un livre de philosophie avant de faire un exo de Maths!
Et comme çà tous le monde gagne à la question 1
oui
tout le monde qui calcule correctement avec Pythagore le trajet qu'il a choisi, qu'il pense être le meilleur.
les perdants sont ceux qui calculent leur trajet en se trompant dans l'application de Pythagore ou dans la soustraction pour avoir BK connaissant HB etc
penser que n'est pas la même chose que être effectivement
philosophie
délire...
il n'y a pas besoin de philosophie pour comprendre des phrases en français !!
mais à l'époque des SMS, du presse bouton et du je veux tout tout de suite on ne comprend plus le français.
ya qu'à mieux écrire les énoncés
il est parfaitement écrit
le seul défaut est que ça va donner plus de travail au correcteur car il devra vérifier les calculs de chacun au lieu de juste comparer automatiquement "la réponse" à un "résultat (unique) attendu"
de toute façon s'il fait son travail sérieusement il ne doit pas se contenter de regarder le résultat final , car on peut très bien obtenir des résultats justes avec des calculs faux (ou des calculs qui font illusion pour faire croire qu'on a obtenu un résultat pompé en fait sur Internet) et alors le résultat étant injustifié doit être considéré comme faux.
Ce qui se conçoit bien s'énonce clairement et les mots pour le dire viennent aisément.
Et les 30 élèves de ma classe pensent la même chose car ils se sont tous dirigés vers des calculs pour essayer de trouver la distance exacte.
Maintenant s'il faut commencer à lire l'énoncé par la fin avant de répondre à la première question faudra penser à mettre un nota bene en début de chapitre.
non justement
(et je pense que c'est ta façon de penser fausse qui a contaminé tes élèves)
relisons cet énoncé dans l'ordre et pas par la fin ni en imaginant qu'on demande autre chose que ce qu'on demande vraiment :
Antonia, claudia et le petit Romain s'amusent beaucoup dans le verger de Pépé José.
le jeu consiste à rejoindre le plus rapidement possible le cerisier en partant de l'abricotier et en touchant le mur.
tout ça c'est une description d'un contexte pseudo réaliste pour "planter le décor"
1.pour augmenter les chances de gagner le jeu, (pour que un enfant de l'histoire gagne à leur jeu) il faudra (futur) que le chemin de la course soit le moins long possible.
là on traduit mathématiquement l'objectif, le but à atteindre par les joueurs de l'histoire, ce qu'on saura faire quand on aura terminé l'exo.
ce n'est pas une question.
c'est l'énoncé d'un but final à atteindre (futur)
à quelle distance du point H peut-on penser qu'il faudra toucher le mur pour que le chemin soit le moins long possible?
ça c'est la question.
et la réponse unique et honnête est bien "je pense que ..." et pas autre chose
si pour penser certains croient que puisque c'est des maths il faut obligatoirement faire des calculs, libre à eux de croire ça (c'est faux)
et ils vont perdre un temps fou et inutile à faire un travail qui n'est pas demandé.
faire une figure à l'échelle dans ce cas OK, dans le cas qu'on a choisi, celui pour lequel on "pense que .."
et calculer la longueur du chemin.
de ce chemin là
ici ce sont les seuls calculs qui sont demandés dans cette question 1 !!!
2.le petit Romain a une idée géniale : etc
suite de l'exo, qui a pour but global de trouver la stratégie pour gagner au jeu de l'histoire.
ici on ne sait toujours pas quelle est la bonne stratéfie, on ne le savait pas dans la question 1, on ne le sait pas plus maintenant
la seule chose qu'on sait :
la stratégie choisie par l'élève (qui ne joue pas vraiment au jeu de l'histoire lui, mais qui pense que pour gagner il faut suivre sa stratégie à lui) :
c'est la réponse à la question 1 elle donne un trajet de longueur calculée question 1
la stratégie de Romain (qui, lui aussi, pense que sa stratégie est la meilleure) : c'est ce qui est dit dans cette question 2
peut être que ce n'est toujours pas la bonne pour espérer gagner au jeu de l'histoire...
qui sait
on le saura à la fin de l'exo.
pour l'instant on s'attache à résoudre cette question 2 telle qu'elle est sans anticiper sur la suite.
etc
avoir lu la fin de l'exo est un bon réflexe car ça peut donner une vision globale de ce qu'est le problème et son but réel et final
mais ça ne veut pas dire qu'il faut utiliser ce qu'on dit dans ces questions suivantes pour résoudre les questions précédentes !!
jamais.
pseudo-réaliste= Relatif à une apparence de réalisme
Si dans mon verger j'ai un cerisier, un abricotier et un mur c'est une pseudo-réalité ?
Moi je vois plutôt çà comme une réalité tout court.
Je vois ce que tu veux dire. Mais bon, c'est un peu pousser mémé dans les orties, c'est du border line en terme de raisonnement pour un enfant de 4ième.
Tout le monde s'appelle pas Gauss. La première question est trop troublante et ambiguë pour un élève moyen. Faut se mettre à la place de l'élève qui a suivi une leçon sur Pythagore et qui se trouve à lire ce genre de problème, on lui parle de distance minimum, de Pythagore. Je crois que son premier réflexe c'est de poser des équations sur sa feuille. Il va pas chercher intuitivement à penser. Saut si la question est formulée plus clairement, du style:
"Intuitivement placer le point H afin de minimiser le parcours à effectuer". Pour des enfants de cet age je pense qu'il convient d'insister et d'écrire clairement. Les questions floues sont à proscrire.
apparence de réalisme :
on déguise le problème de fond (distance minimale) sous la forme d'une histoire fictive de gamins qui jouent dans un verger
quelle différence subtile de "philosophe tordu" entre
"placer intuitivement" et "où pensez vous que" ..
pour n'importe qui du commun des mortels c'est exactement la même chose.
ce n'est pas flou du tout.
Bon ok, si le verbe placer=penser j'arrête de suite;
On est pas ds le même monde et on doit pas avoir le même dictionnaire.
A vous entendre parler on peut maintenant affirmer que les livres d'école de maths de nos ancêtres ont été écrit par des cons. Et que ceux utilisés aujourd'hui dans nos classes ont été écrit par une élite et seulement destinés à une élite.





