Inscription / Connexion Nouveau Sujet
Pythagore dans une sphère
Bonjour,
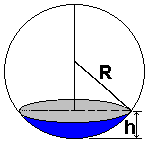
Je voudrais comprendre pourquoi sur cette sphère on a R² = r²+h²
R étant le Rayon de la sphère,r le rayon du disque.
Je ne sais pas si c'est un problème de perspective mais quand j'essayer d'écrire r en utilisant Pythagore je me plante
je trouve
R²=(R-h)²+r²
R²=R²+h²-2RH+r²
r²=2Rh-h²
et non r²=R²-h² :/
Merci d'avance 
Bonsoir,
d'où sors-tu cette relation ?
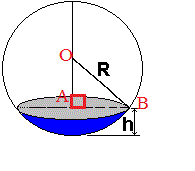
elle serait vraie si h était la distance du centre au disque gris or ici ce n'est pas le cas....
http://fr.wikipedia.org/wiki/Volume_d'une_sph%C3%A8re
http://homeomath.imingo.net/integral13.htm
Voici des liens 
il me semble, mais ce n'est pas très clair, que, d'après le second site, z est la cote du disque
z varie de - R à R
il y a peut-être une erreur pour h sur le 1er site : telle qu'indiquée sur le dessin h varierait plutôt de 0 à 2R
mais je peux me tromper....
Mais en utilisant l'intégrale entre -R et R de 
on trouve

Qui est bien le volume de la sphère
R²-h² étant r² qui représente l'aire d'un petit disque et en même temps son volume d'après ce que j'ai lu :p
ça doit être un problème de perspective dans la sphère :/
Merci
Non, c'est un problème de définition de ce qu'est h ...
un coup c'est la distance au centre, un coup la distance au pole (sud) etc faut pas tout mélanger.
l'aire d'un petit disque et en même temps son volume d'après ce que j'ai lu
volume du disque =
 r² dh
r² dhSalut
Non, c'est un problème de définition de ce qu'est h ...
un coup c'est la distance au centre, un coup la distance au pole (sud) etc faut pas tout mélanger.
Tu pourrais me faire un schéma parce que je te suis pas :S
Merci
c'est clair
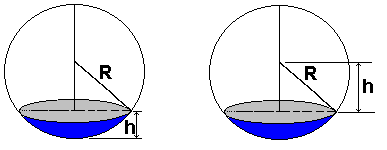
selon que tu définis h comme étant la hauteur de la calotte (1er dessin) donc la distance du disque "au pole sud",
ou bien que tu définis h comme la distance au centre (2eme dessin) les calculs sont différents
dans un cas tu dois intégrer pour h entre 0 et 2R
dans l'autre entre -R et +R
et les formules r = f(h) sont différentes puisque ce n'est pas le même h !!
chercher à comparer des résultats intermédiaires de l'un (r = f(h) aux résultats intermédiaires de l'autre n'a aucun sens.
il faut poursuivre les calculs jusqu'au bout dans le cas qu'on a choisi.



