Inscription / Connexion Nouveau Sujet
Rectangle, cercle et fonction.
Bonjour,
Je travaille sur un exercice dont l' énoncé est :
Un rectangle ABCD est inscrit dans un demi-cercle de centre O , de diamétre [i,j] et de rayon 4 cm. On note la mesure en radian de l'angle BOC telle que
La première question consistais a démontrer que :
et la deuxième est : "Déterminer pour quelles valeurs de l' aire d u triangle ABCD est la plus grande et donner alors les dimensions de ce rectangle.
J' ai l' intuition que l' aire du rectangle ABCD est maximale pour
comme ca on aurait et ainsi une aire de 16.cm²
mais je ne trouve pas comment la démontrer irréfutablement, j' ai pensé a l' extremum mais je n' y arrive pas forcement, il y a t-il une vraie solution afin de montrer le résultat ?
Merci d' avance.
Bonjour,
soit de façon verbale en expliquant les variations de la fonction composée sin(2
) à partir des variations (connues) de sin(u) et de u = 2, connue aussi
soit formellement en calculant la dérivée et signe de cette dérivée et tableau de variations ...
(dans l'intervalle défini par l'énoncé)
Merci , ça marche bien !
La dernière question est : "montrer qu'il existe deux valeurs de pou lesquelles l' aire ABCD est de 10 cm². Donner les valeurs de
à 10^-1 près.
Je ne suis pas sur d' appliquer la bonne méthode , sur le dessin ça se voit parfaitement .
Je fait
je suis tenté de rajouter a mon résultat pour obtenir ma deuxième solution mais je ne trouve pas de résultat vraiment cohérent , avez vous une piste ?
résoudre sérieusement
sin(2) = sin(a) (en posant a = ce que tu as calculé)
et pas "ajouter pi/2" ou je ne sais quoi à tort et à travers "au flan".
tu dois savoir que résoudre sin(x) = sin(a) donne x = a ou x = pi - a, modulo 2pi
il doit y avoir quelque chose qui m' échappe :
donc x= 9.65 ou
alors que j' ai trouvé via la calculette que je devrais trouvé 0,34
?
faut pas mélanger des mesures en radian et en degré
soit tu écris tout en radian, soit tout en degré (pi radian = 180°)
(et toujours préciser les unités, ça évitera de retrancher xxx degrés à pi radians)
faut pas non plus mélanger et 2
a c'est arcsin(10/18) point final pas la moitié !
sin(2) = 10/18 = sin(33.75°)
donc 2 = 38.7° (la première solution = 38.7/2 = 19.3 °)
ou 2 = 180° - 33.75° = ... et donc l'autre solution = ... °
On à alors
Merci , je comprend mieux la méthode! 
seulement si je fait :
Qui est tout de même assez éloigné de 10 c' est donc normal ?
au lieu de recopier mes valeurs tu devrais faire tes propres calculs avec le principe indiqué.
le simple fait que j'écrive une fois 33.75 une fois 38.7 pour le même angle aurait dû te mettre la puce à l'oreille que le 18 au lieu de 16 n'était finalement pas la seule faute de frappe ...
(et ça ne va pas s'arranger côté fautes de frappe vu que la plus grande partie du temps consacré à répondre est occupé par l'attente de réponses de client.google, de facebook, de estat etc etc qui plombent le chargement des pages du site, et parfois l'empêchent, causant la perte du message en cours de frappe)
Ça y est c' est sur :
Merci !!.
Oui , Ça m' arrive aussi de tout perdre au dernier moment et de devoir réécrire le message !
bis répetita ...
faut pas non plus mélanger
et 2reprenons mon message bourré de fautes de frappes :
a c'est arcsin(10/16) point final pas la moitié !
sin(2
) = 10/16 = sin(38.7°)
donc 2
= 38.7° (la première solution = 38.7/2 = 19.3 °)
ou 2
= 180° - 38.7° = ... et donc l'autre solution = ...
et pas ta valeur absurde (entre 0 et 90° !!! dit l'énoncé)
et même en divisant par deux fausse.
Bon je m' y suis remis a tête reposée, c' était un carnage.
On trouve finalement :
Merci de votre patience.
J' ai du revoir les équations trigonométrique, ça m' était totalement sorti de la tête. J' ai vu que c' était au programme de première S et je me souvenais même pas en avoir fait. ...
Merci
Oui,
mais pas modulo 2
puisque l'énoncé dit que 0 
90° (pi/2 radians)
on ne cherche donc les solutions que dans cet intervalle
et puis
d'une part c'est 2 qui est modulo 2
sin(2) = sin(
) donne dans 
2 = modulo 2 donne
= /2 modulo seulement, pas 2
et pareil pour l'autre solution 2 = - modulo 2
= (-)/2 modulo
d'autre part comme tu donnes les angles en degrés, de toute façon ce serait modulo 180° 
en prime une petite construction géométrique "sans calculs" :
(ça permet d'obtenir, si on fait cette construction avec Geogebra ou avec soin, une mesure indépendante de pour vérifier les calculs... )
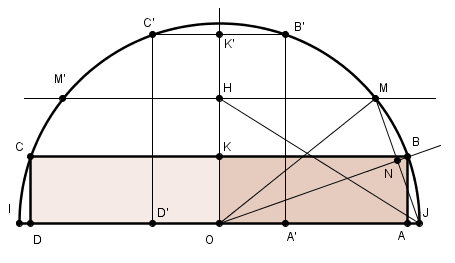
on veut aire ABCD = 10 cm² donc par symétrie aire de OABK = 5cm²
en découpant en deux et en réarrangeant les morceaux (OAB = OJN = OMN)
aire de OABK = aire de OJM ou M est le symétrique de J par rapport à OB
d'où la construction :
construire H de sorte que le triangle OJH ait pour aire la moitié de l'aire donnée (= 5cm²) donc OH = 5/4 = 2.5 cm
la parallèle à IJ en H coupe le cercle en M (et M'). Les triangles OJM et OJH ont même base et même hauteur, donc même aire 5cm²
la médiatrice de JM coupe le cercle en B cherché et on complète le rectangle ABCD
l'autre solution est obtenue de même avec M'
ou par symétrie autour de la 1ère bissectrice, les rectangles OABK et OA'B'K' étant isométriques, même dimensions, même aire donc.
Annuler
connectez vous