Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques Collège cycles 3 /4On parle exclusivement de maths, niveau collège. TroisièmeForum de troisième Racines carréesTopics traitant de racines carrées [tout]Lister tous les topics de mathématiques
Niveau troisième
Partager :

Rectangle d'or

Posté par
Louisa59 12-10-09 à 20:42

Bonsoir

Notre professeur nous a donné à réfléchir sur cette phrase : On appelle rectangle d'or un rectangle tel que le quotient de sa longueur par sa largeur est égal au nombre d'or.

J'ai cherché sur le net, le nombre d'or est égal à (1 + 5)/2.

Mais je n'arrive pas à démontrer qu'un rectangle est un rectangle d'or. Je comprends d'après la définition du rectangle d'or que L/l = (1 + 5)/2.

Je sais pas si je me suis bien exprimée.

Pouvez-vous m'expliquer, mais il n'a rien de pressant, c'est juste une réflexion pour mercredi.

Merci

Posté par
gwendolinre : Rectangle d'or 12-10-09 à 21:38

Bonjour,

Je pense que il suffit de dire que L=1+V5 et l=2

ou L=2(1+V5) et l=4

et ainsi de suite

Posté par
Daniel62re : Rectangle d'or 12-10-09 à 21:49

Bonsoir,

pas compris Louisa

qu'est-ce que tu dois démontrer ?

que le rectangle est un rectangle d'or, mais tu n'as pas de données ?

ou pourquoi on l'appelle rectangle d'or ?

Posté par
Louisa59re : Rectangle d'or 12-10-09 à 22:02

Bonsoir à vous 2

Je ne vous comprends pas !

Je dois démontrer qu'un rectangle est un rectangle d'or

Posté par
gwendolinre : Rectangle d'or 12-10-09 à 22:04

je t'ai mis les conditions pour plus haut

L/l=(1+V5)2
signidie que L=1+V5 et ses multiples et l=2 et ses multiples

Posté par
Louisa59re : Rectangle d'or 12-10-09 à 22:09

Ok gwendolin

je vais donner les conditions que tu m'as décrites

Merci

Posté par
olive_68re : Rectangle d'or 12-10-09 à 22:17

Salut à tous

Il faut quand même encore préciser que les multiples doivent être les mêmes en haut et en bas

Parce que 3$\fr{2(1+\sqrt{5})}{3\times 2} ça ne va pas

Les rectangles d'or ont donc pour longeur 3$\cal{L}=k\times (1+\sqrt{5}) et pour largeur 3$\ell =k\times 2 où 3$k est un entier naturel .

Posté par
Louisa59re : Rectangle d'or 12-10-09 à 22:39

Coucou olive

J'ai trouvé un exemple :

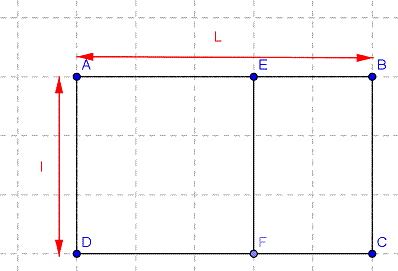
Le rectangle ci-dessous est un rectangle d'or.

On a construit le point E du segment [AB] et le point F du segment [DC] de telle façon que le quadrilatère AEFD soit un carré.

Démontrer que le rectangle BCFE est aussi un rectangle d'or

Rectangle d\'or

Posté par
Daniel62re : Rectangle d'or 12-10-09 à 22:42


Définition de la proportion d'or:
Deux longueurs strictement positives a et b respectent la proportion d'or
si et seulement si, le rapport de a sur b est égal au rapport de a + b sur a :
\rm \frac{a}{b} = \frac{a+b}{a}

si ton rectangle a pour dimensions:
a =1+5  et b=2

\rm \frac{a+b}{a} = \frac{1+\sqrt{5}+2}{1+\sqrt{5}} = \frac{3+\sqrt{5}}{1+\sqrt{5}} = \frac{(3+\sqrt{5})(1-\sqrt{5})}{(1+\sqrt{5})(1-\sqrt{5})} = \frac{3-3\sqrt{5}+\sqrt{5}-5}{1-5} = \frac{-2-2\sqrt{5}}{-4} = \frac{1+\sqrt{5}}{2}

ses dimensions sont en proportion d'or
voilà pourquoi on l'appelle rectangle d'or

Rectangle d\'or

Posté par
Louisa59re : Rectangle d'or 12-10-09 à 22:53

Merci et bonne nuit

Posté par
plumemeteorere : Rectangle d'or 12-10-09 à 22:54

Bonjour Louisa.
AB/BC = BC/EB
comme BC = AE : AB/AE = AE/(AB-AE)
en prenant comme unité de mesure la largeur du grand rectangle AE = 1 :
AB = 1/(AB-1).
AB est un nombre positif tel qu'en lui retranchant 1 on obtient son inverse.
(V5+1)/2 répond à cette condition.
En effet : (V5+1)/2 - 1 = (V5+1)/2 -2/2 = (V5-1)/2.
Ce nombre est l'inverse de (V5+1)/2.
En effet :
(V5+1)/2 * (v5-1)/2 = (V5*1)(V5-1)/4 = (5-1)/4 = 1.

Supplément.
Construction d'un rectangle d'or.
On part de la largeur et on construit le carré AEFD ayant pour côté cette largeur.
On trace le cercle de diamètre [EF] de centre O.
La demi-droite [DO) traverse le cercle en M puis en N.
DM sera la largeur du petit rectangle (EBCF) de ta figure; DN sera la longueur du grand rectangle de ta figure.

Posté par
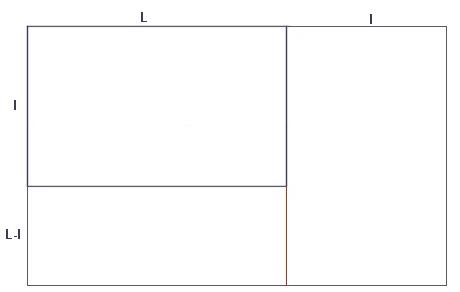
Daniel62re : Rectangle d'or 12-10-09 à 22:57

remarque que:

  \rm \frac{a}{b} = \frac{a+b}{a}

      

  \rm \frac{l}{L-l} = \frac{L}{l}

bonne nuit

Posté par
Louisa59re : Rectangle d'or 12-10-09 à 22:58

Bonsoir plumemeteore

ouh là ! j'ai plutôt intérêt à copier et à relire cela à tête reposée.

Merci

Posté par
Louisa59re : Rectangle d'or 12-10-09 à 23:06

Excuse-moi Daniel

Mais comment tu trouves ça ?

\rm \frac{l}{L-l} = \frac{L}{l}

Posté par
Daniel62re : Rectangle d'or 12-10-09 à 23:15

j'ai égalisé:
  L=a+b et l=a

donc b = L-a = L-l
et a/b = l/(L-l)

je suis parti de a/b donc L/l
en prouvant que L/l = (L+l)/L

tu es parti de L/l
en prouvant que l\(L-1) = L/l

c'est la même chose mais à l'envers
j'ajoute l à L avec un carré L sur L pour avoir un rectangle d'or

tu retranches l de L avec un carré l sur l pour avoir un rectangle d'or

on peut répéter l'opération à l'infini dans les deux sens.

Posté par
Daniel62re : Rectangle d'or 12-10-09 à 23:16

je corrige:

tu es parti de L/l
en prouvant que l\(L-l) = L/l

Posté par
Louisa59re : Rectangle d'or 12-10-09 à 23:22

Merci Daniel

ça se complique là les maths

par la suite je vois qu'on peut reproduire la coquille du nautile à partir d'une série de rectangles d'or

mais je vais m'arrêter

Merci

Posté par
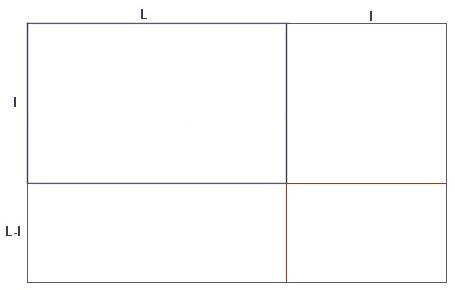
Daniel62re : Rectangle d'or 12-10-09 à 23:28

Rectangle d\'or

en prolongeant la ligne du milieu (en rouge) je retrouve le rectangle d'or l/(L-l)

il y a 3 triangles d'or dans la figure
l'original c'est L/l
le grand c'est (L+l)/L
et l/(L-l)

Posté par
Daniel62re : Rectangle d'or 12-10-09 à 23:29

il y a 3 rectangles d'or dans la figure

Posté par
Daniel62re : Rectangle d'or 12-10-09 à 23:31

les proportions sont respectées

Posté par
Louisa59re : Rectangle d'or 12-10-09 à 23:48

Merci

Et cette fois-ci, bonne nuit

Posté par
Daniel62re : Rectangle d'or 12-10-09 à 23:49

on note le nombre d'or

1,618

une propriété du nombre d'or:

  \rm \phi = 1 + \frac{1}{\phi}

\rm si \frac{L}{l} = \phi:

  \rm \phi = \frac{L}{L} + \frac{l}{L}

un rectangle d'or peut se découper en un carré et un rectangle d'or

Posté par
Louisa59re : Rectangle d'or 12-10-09 à 23:54

donc pour le nautile, j'augmenterai les proportions au lieu de les diminuer, c'est ça ?

Posté par
Louisa59re : Rectangle d'or 12-10-09 à 23:55

oh puis non, je dis n'importe quoi là, c'est vrai que je peux aussi partir d'un grand rectangle pour en arriver à un trés petit et là je pourrais inscrire le nautile

Posté par
Daniel62re : Rectangle d'or 12-10-09 à 23:56

oui il vaut mieux diminuer

et obtenir des rectangles de plus en plus petits

Posté par
Louisa59re : Rectangle d'or 12-10-09 à 23:58

Bon bien ça je l'ai au moins compris

Merci à toi Daniel et merci surtout pour ta patience, c'est des fois laborieux je le reconnais

Posté par
Daniel62re : Rectangle d'or 13-10-09 à 01:56

je refais la démonstration pour prouver que:

"un rectangle d'or peut se découper en un carré et un rectangle d'or"

soit le nombre d'or

soit un rectangle de Longueur a et de largeur b

a et b respectent la proportion d'or:

   \rm \frac{a}{b} = \frac{a+b}{a}

   \rm \frac{a}{b} = \frac{a}{a} + \frac{b}{a}

   \rm \phi = 1 + \frac{1}{\phi }

   \rm \phi - 1 = \frac{1}{\phi }

   \rm \frac{a}{b} = 1 + (\frac{a}{b} - 1)

   \rm \frac{a}{b} = 1 + (\frac{a}{b} - \frac{b}{b})

   \rm \frac{a}{b} = 1 + (\frac{a-b}{b})


   \rm \frac{a}{b} = \frac{b}{b} + (\frac{a-b}{b})
   \rm \frac{a}{b} = \phi %20= 1 + (\phi - 1) = 1 + \frac{1}{\phi }

  \rm avec \frac{a}{b} = \phi %20: le rectangle d'or

  \rm avec \frac{b}{b} : un carre

  \rm avec \frac{a-b}{b} = \frac{1}{\phi } : un rectangle d'or


en multipliant par b² on retrouve les surfaces:

   \rm \frac{ab^2}{b} = \frac{bb^2}{b} + (\frac{b^2(a-b)}{b})

   \rm ab = b^2 + b(a-b)

   surface du rectangle d'or = surface d'un carré + surface d'un rectangle d'or

Posté par
Louisa59re : Rectangle d'or 13-10-09 à 09:15

Bonjour

j'ai trouvé beaucoup d'explications ici   [lien]  je n'avais pas pensé à regarder dans l'encyclopédie

Merci pour tous ces détails

Posté par
enolaweirdre : Rectangle d'or 03-01-15 à 09:07

Bonjour! (et bonne année!)
Je suis intéressée par ce problème car j'ai le même à résoudre (démontrer qu'un rectangle est rectangle d'or sachant qu'il est fait à partir d'un carré...)
Il y a cependant une chose que je n'ai pas comprise :

Citation :
je suis parti de a/b donc L/l
en prouvant que L/l = (L+l)/L

J'ai beau relire, je ne saisis pas le cheminement..
Pouvez-vous m'expliquer?
Merci

Posté par
mathafou Moderateurre : Rectangle d'or 03-01-15 à 10:28

Bonjour,
tout ce topic entier est basé sur un malentendu au départ : comment montrer quelque chose à partir d'un énoncé absent !

en d'autres termes :

Citation :
sachant qu'il est fait à partir d'un carré...
ne veut rien dire du tout
comment est il fait à partir de ce carré, quelle est la construction exacte de l'énoncé, figure comprise.
parce que là il y a des tonnes de façons différentes de monter qu'un rectangle est un rectangle d'or, selon la façon exacte dont il a été construit.
peut être par la formule que tu cites, peut être pas...

Posté par
dpire : Rectangle d'or 03-01-15 à 10:50

Bonjour,

On connait la définition Longueur/largeur =
Construction:
On part du carré de coté 1

on prend une médiane de base O  on trace une oblique vers un coté du carré
Le cercle correspondant à ce rayon coupe le prolongement du
coté portant O ,ainsi le coté du rectangle est créé.

Passons au chiffres:
1/2 coté = 1/2
le rayon issu de O est l'hypoténuse
soit R=(1+ (1/2)²)
et donc L=(1/2)+R
soit 1/2+1.25=1.618033 =

Rectangle d\'or

Posté par
mathafou Moderateurre : Rectangle d'or 03-01-15 à 11:32

si c'est bien comme ça qu'a été défini ce rectangle dans cet exo ...

Posté par
enolaweirdre : Rectangle d'or 03-01-15 à 12:53

Je vous remercie pour vos réponses, je pense avoir compris!
En re-consultant l'encyclopédie j'ai revu cette formule (c'était uniquement ça qui me posait problème) en faisant des exercices en lignes. Merci cependant pour le schéma, il m'a beaucoup aidé!

Posté par
plumemeteoreêtre 03-01-15 à 13:49

Bonjour.être é
Il faudrait encore prouver géométriquement que le grand rectangle et le rectangle de droite ont le même rapport de côtés.
Cela m'agace que l'on dise aux élèves que la définition du nombre d'or est d'être égal à (√(5+1))/2. La vraie définition est, en substance, le rapport de deux nombres formant une progression géométrique avec leur somme. La valeur exacte de ce rapport n'est qu'une conséquence de cette définition.

Posté par
enolaweirdre : Rectangle d'or 03-01-15 à 15:34

Bonsoir,
C'est vrai que c'est la valeur "brute" qu'on lui donne...Si il y d'autre moyens de le concevoir je suis preneuse! C'est toujours utile...

Posté par
dpire : Rectangle d'or 04-01-15 à 10:15

Bonjour,

L'avantage du rectangle d'or c'est
justement que cette constante s'applique
au rectangle restant après découpage du carré.

En partant de la construction basique l=1
et après mesure L=
On doit donc vérifier pour le "noir".
l1=-l
L1=1
L1/l1 =


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !