Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Géometrie plane et dans l'espaceTopics traitant de Géometrie plane et dans l'espace [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Rectangle inscrit dans un cercle d'aire maximale

Posté par
Lou0115 27-10-23 à 11:57

Bonjour, je suis en terminale et je bloque sur cet exercice, pouvez-vous m'aider s'il vous plait ?

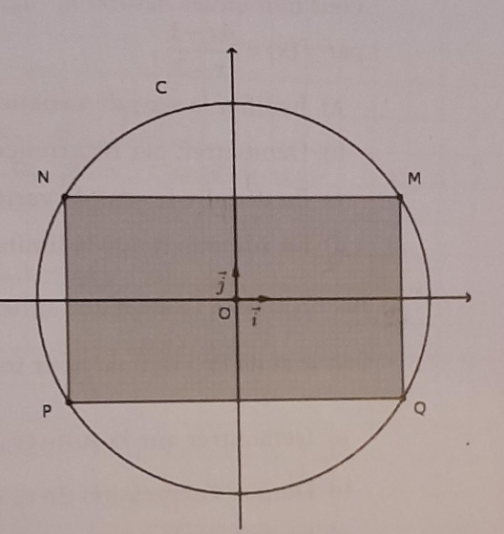
Le plan est muni d'un repère orthonormé (O; i; j).

Sur la figure ci-contre, le point M est mobile sur le cercle C de centre O et de rayon 5,

Le point M reste sur le quart de cercle laissant ses coordonnées (x ; y) positives. On construit alors le rectangle MNPQ Inscrit dans le cercle C.



1) Soit A(x) l'aire du rectangle MNPQ exprimée en fonction de l'abscisse x du point M. Montrer que A(x) = 4x 25-x²

2) La fonction A(x) est définie sur l'intervalle [0: 5] et dérivable sur [0; 5[

Calculer A'(x) et en déduire les variations de A. Les résumer dans un tableau,


3) Pour quelle valeur exacte de x l'aire de MNPQ est-elle maximale?
Quelle particularité présente alors le rectangle MNPQ?

Pour la question 1, je pense avoir compris le raisonnement mais ce qui me gène c'est les coordonnées de M.

Rectangle inscrit dans un cercle d\'aire maximale

Posté par
malou Webmasterre : Rectangle inscrit dans un cercle d'aire maximale 27-10-23 à 12:19

Bonjour

petit dépannage en passant...
on te dit que M a pour abscisse x
tu sais que M est sur ce cercle parfaitement connu, donc tu peux trouver l'ordonnée de M en fonction de x comme demandé

Posté par
Pirhore : Rectangle inscrit dans un cercle d'aire maximale 27-10-23 à 12:25

Bonjour,

@malou: toujours plus rapide que moi

Posté par
Lou0115re : Rectangle inscrit dans un cercle d'aire maximale 27-10-23 à 14:31

malou Merci pour votre réponse, donc si j'ai bien compris je vais devoir utiliser le théorème de Pythagore.  Mais est-ce que je peux écrire ça : x²+y² = 10² ?

Posté par
fabo34re : Rectangle inscrit dans un cercle d'aire maximale 27-10-23 à 14:58

Bonjour. Tu as le droit d'utiliser ton cours de 1ère.

Dans un repère orthonormé, un point M(x;y) est sur le cercle de centre C(x_C;y_C) et de rayon R,  alors:

CM^2=(x-x_C)^2+(y-y_C)²=R^2

C'est un résultat qui est effectivement la conséquence du théorème de Pythagore, mais il ne faut pas tout le temps tout redémontrer

Dans ta formule, c'est donc 5², et pas 10²

Posté par
Lou0115re : Rectangle inscrit dans un cercle d'aire maximale 27-10-23 à 15:11

fabo34 Merci pour votre réponse, cependant j'avais écrit 10² car je souhaitais appliquer le théorème de Pythagore sur le rectangle MNPQ et comme le rayon est 5, le diamètre est 10. Néanmoins je ne sais toujours pas comment faire pour calculer l'aire de ce rectangle pouvez m'expliquer ?

Posté par
Pirhore : Rectangle inscrit dans un cercle d'aire maximale 27-10-23 à 15:18

quelle est l'ordonnée du point M?

Posté par
Lou0115re : Rectangle inscrit dans un cercle d'aire maximale 27-10-23 à 15:34

Pirho @ 27-10-2023 à 15:18

quelle est l'ordonnée du point M?

C'est y ?

Posté par
Lou0115re : Rectangle inscrit dans un cercle d'aire maximale 27-10-23 à 16:08

Pirho @ 27-10-2023 à 15:18

quelle est l'ordonnée du point M?
ou alors c'est peut être :
x² +y² = 5²
y² = 25 - x²
y=25-x²
Mais je ne suis pas sûr

Posté par
Pirhore : Rectangle inscrit dans un cercle d'aire maximale 27-10-23 à 16:48

en toute rigueur tu devrais écrire  y=\pm\sqrt{25-x^2}

mais pour la partie du cercle reprise sur la figure c'est juste ; donc M(x;\sqrt{25-x^2})

et l'aire du rectangle vaut?

Posté par
Lou0115re : Rectangle inscrit dans un cercle d'aire maximale 27-10-23 à 17:43

Pirho @ 27-10-2023 à 16:48

en toute rigueur tu devrais écrire  y=\pm\sqrt{25-x^2}

mais pour la partie du cercle reprise sur la figure c'est juste ; donc M(x;\sqrt{25-x^2})

et l'aire du rectangle vaut?


Merci beaucoup pour votre aide
Oui le résultat d'une racine carrée peut-être positif ou négatif mais ici on ne peut pas avoir de résultat négatif.
Donc l'aire du petit rectangle vaut x25-x²
Ainsi l'aire du rectangle MNPQ vaut 4 x25-x²
Néanmoins je ne sais pas si ma rédaction est correcte

Posté par
Pirhore : Rectangle inscrit dans un cercle d'aire maximale 27-10-23 à 19:52

pour moi, c'est correct

Posté par
Lou0115re : Rectangle inscrit dans un cercle d'aire maximale 27-10-23 à 20:25

Pirho @ 27-10-2023 à 19:52

pour moi, c'est correct

Très bien merci beaucoup !!!

Posté par
Sylvieg Moderateurre : Rectangle inscrit dans un cercle d'aire maximale 28-10-23 à 07:11

Bonjour,
Juste une remarque :
Le résultat d'une racine carrée est toujours positif ou nul.
Par contre, une des deux solutions de x2 = 2023 est négative
.

Posté par
Pirhore : Rectangle inscrit dans un cercle d'aire maximale 28-10-23 à 08:08

Bonjour Sylvieg,

Sylvieg @ 28-10-2023 à 07:11


Le résultat d'une racine carrée est toujours positif ou nul.

tout à fait d'accord avec toi mais pour la partie "inférieure" du cercle on a bien y=-\sqrt{25-x^2}

Posté par
Lou0115re : Rectangle inscrit dans un cercle d'aire maximale 02-11-23 à 15:27

Pirho @ 28-10-2023 à 08:08

Bonjour Sylvieg,

Sylvieg @ 28-10-2023 à 07:11


Le résultat d'une racine carrée est toujours positif ou nul.

tout à fait d'accord avec toi mais pour la partie "inférieure" du cercle on a bien y=-\sqrt{25-x^2}


Mais y n'est pas plutôt égal à ça : y = 25-x²   ??

Posté par
Sylvieg Moderateurre : Rectangle inscrit dans un cercle d'aire maximale 02-11-23 à 15:42

Oui, c'est bien ça.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !