Inscription / Connexion Nouveau Sujet
Récurrence sur suite définie par une fonction.
Bonjour,
J'ai un problème qui me parait "évident", mais pourtant je bloque complètement pour le démontrer. Si quelqu'un peut m'éclairer je lui serais très reconnaissant ^^
Soit (un) la suite définie par :
- u0 = 8
- un+1 = f(un)
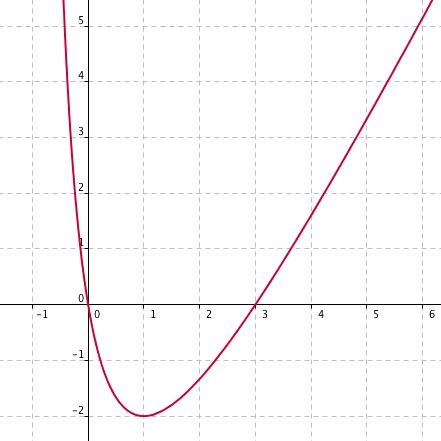
Avec f(x) = (2x²-6x) / (x+1) définie sur IR\{-1}.
(j'ai étudié son sens de variation dans une question précédente, elle est :
- croissante entre -infini et -3,
- décroissante etre -3 et 1 ,
- puis croissante de de 1 à +infini.)
Il s'agit de montrer que (un) est croissante.
J'ai pensé à le faire par récurrence :
Soit P la proposition suivante : Quelque soit un entier naturel n, un+1 > un.
au rang n=0 :
u0 = 8
u1 = f(8) = 8.89 Donc ok.
Là où je bloque, c'est pour la suite...
Supposons que P est vraie au rang n, c'est à dire un+1>un.
On veut démontrer que c'est vrai au rang n+1, et donc que un+2>un+1.
J'ai envie de dire que par hypothèse, un+1>un, et comme f est croissante on a f(un+1)>f(un)....
Mais je n'ai aucune certitude qu'on se trouve bien sur un intervalle où f est croissante...
Pourtant ça parait évident que si le premier terme (8) est supérieur à 1, alors tous les termes de la suite seront dans un intervalle ou f sera croissante. Mais je n'arrive pas du tout à l'exprimer..
Voila, en vous remerciant de m'avoir lu =)
Bonjour,
- croissante entre -infini et -3,
- décroissante etre -3 et 1 ,
- puis croissante de de 1 à +infini.)
Je ne crois pas, non.
Ah ... Je poste mon calcul :
Je calcule la dérivée de f(x) :
f'(x) = [ (4x - 6)*(x+1) - (2x²-6x) ] / (x+1)²
= (4x² -6x +4x -6 -2x² -6x) / (x+1)²
= (2x² -8x -6) / (x+1)²
Du coup j'étudie le signe du dénominateur : les racines sont ah... oui déjà je me suis trompé à ce niveau..
Bon je vais voir si ça change quelque chose, merci !! =)
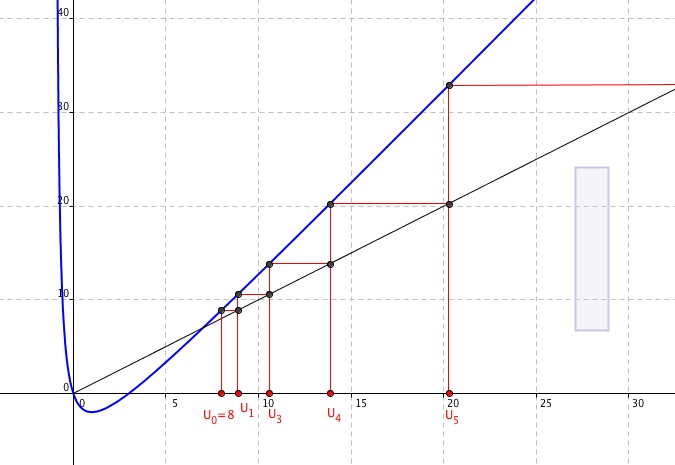
Merci pour la courbe, !!
Mais du coup, comment affirmer que f est croissante dans ma preuve de récurrence.... et être sûr qu'on ne se trouve pas dans un intervalle décroissant ? :/
Oui, je trouve :
f'(x) = [ (4x - 6)*(x+1) - (2x²-6x) ] / (x+1)²
= (4x² -6x +4x -6 -2x² +6x) / (x+1)²
= (2x² +4x -6) / (x+1)²
Comme le dénominateur est tjs positif, ça revient à étudier le signe du numérateur.
Les racines sont -3 et 1.
Donc f' est de signe positif à l'extérieur des racines, et négatif à l'intérieur,
donc f est croissante sur ]-inf, -3]
décroissante sur ]-3, -1[ U ]-1, 1[
et croissante sur ]1, +inf[
Mais du coup je retrouve bien la même chose, et je n'arrive toujours pas à dire pourquoi f serait croissante pour réussir à prouver la récurrence.... En plus j'ai l'impression que c'est trivial car ça ne pose de problème qu'à moi, mais j'arrive vraiment pas à avoir le déclic 
Tu confonds "fonction positive" avec "fonction croissante", et "fonction négative" avec "fonction décroissante".
Bon je m'aperçois que je t'ai induit en erreur.
Elle est effectivement :
- croissante entre -infini et -3,
- décroissante etre -3 et 1 ,
- puis croissante de de 1 à +infini.
Enfin de compte, j'ai eu ma réponse : Ce qui ne tenait pas la route, c'est ma proposition de récurrence.
Plutôt que de seulement chercher à montrer que : un+1 un
un
Il suffit de poser P(n) la proposition : un+1 un
un 8
8
Et du coup tout va bien, on est bien sur un intervalle ou la fonction est croissante, on peut donc déduire de l'hypothèse que f(un+1)  f(un) \o/
f(un) \o/
Merci Jedoniezh pour le temps que tu as passé en tout cas !! =)