- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
Regression polynomiale (Parabolique)
Hello,
Je cherche un moyen de caler au mieux une parabole dans le nuage de points qui la décrit.
La même chose qu'une droite quand on parle de régression linéaire (méthode des moindres carrés) sauf que là il s'agit d'une parabole comme je le disais.
Donc pas de soucis en ayant lu ceci j'y arrive.
http://www.ac-nancy-metz.fr/enseign/physique/divers/MethodNum/Schw-doc/RegPoly02.pdf
(En passant il y a une petite erreur pour Delt|M|)
Ce que je souhaiterai maintenant c'est calculer le coefficient de corrélation R, mais là ils n'en parlent pas.
Par contre dans la page ci-dessous R est donné et il ne me semble pas qu'il soit uniquement destiné à une régression linéaire.
http://fr.wikipedia.org/wiki/Corrélation_(statistiques)
Je pense que ça doit aussi être applicable pour une parabole ou tout autres courbes. Cependant j'ai un doute car quand je le calcul avec des points appartenant exactement à une parabole, R=0.96...... et non pas 1 ou -1.
Avez-vous une idée pour que je sache si c'est bien ça ou s'il prend une autre forme ?
Merci.
Bonjour,
Sans avoir regardé de près, le texte du wiki précise bien "Coefficient de corrélation linéaire de Bravais-Pearson", et linéaire est en italique, ce n'est probablement pas par harasd...
Oui, effectivement c'est pas ça.
J'ai testé sous excel des points appartenant à la parabole et la fonction "Courbe de Tendance" me renvoie R = 1
J'ai pourtant bien fouillé sur le net mais je ne trouve pas l'expression de R pour une régression parabolique.
Je vais donc voir comment il est calculer pour une droite et je vais tenté de l'appliquer dans le cas d'une parabole.
Mais si toute fois vous avez des pistes....  je suis preneur.
je suis preneur.
Bye
Oui, j'avais déjà consulté ce site à plusieurs reprises, mais sans trouver exactement ce que je cherchais, par contre il m'a mis sur la bonne piste. Il y est dit à un endroit qu'une régression d'ordres multiples à 1 variable (x²) pouvait également être considérée comme une régression à multiples variables (x, y, z)
J'ai donc cherché et trouvé l'info souhaitée : (Voir image ci-dessous)
Où
Yi représentent les valeurs mesurées (Nuage de points)
Y_ est la moyenne pondérées des Yi
Yi^ représentent les valeurs calculées décrivant la courbe.
Je laisse donc l'info sur le forum. Quelqu'un recherchera peut-être la même chose plus tard.
Merci LeHibou pour m'avoir aiguillé.
Bye.
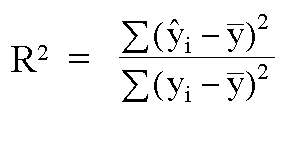


 statistiques en post-bac
statistiques en post-bac