Inscription / Connexion Nouveau Sujet
Remontée de l'algorithme d'Euclide
Bonjour !
J'ai un exercice de maths que je réussis pas à terminer et je vous demande votre aide (enfin surtotu une explication pour m'aider ) je vous remercie par avance
Un élève a déterminer le PGCD de a et b par l'algorithme d'Euclide. Voici le tableau qu'il a réalisé, mais quelques nombres on été effacés. Trouvez quel est le nombre b ( avec b < 5915)
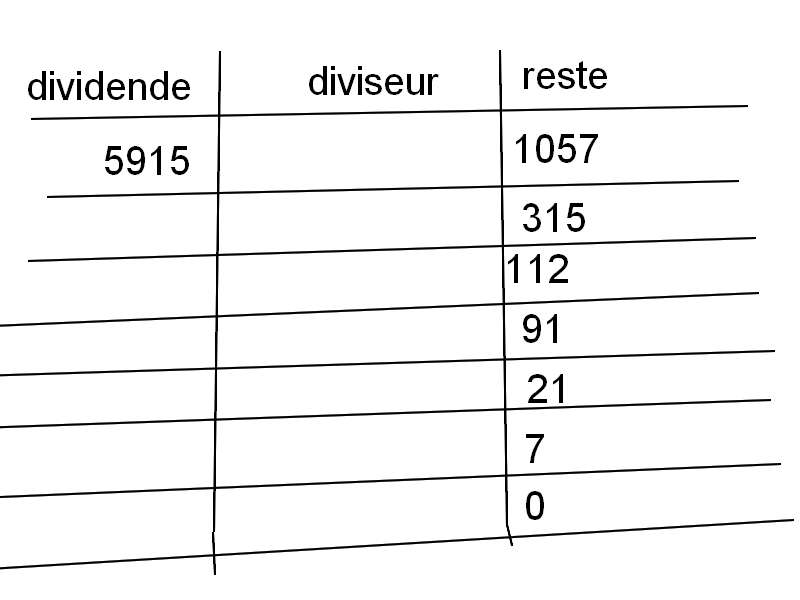
J'ai joint le tableau.
En fait j'ai réussi à remonter jusqu'à la 2ème ligne où je reste bloquée car je n'ai pas de dividence.
Merci d'avance.
Bizz
Bonsoir Liadan et Daniel.
Dans la première division, si le dividende diminuait de 1057, le reste serait 0 et le quotient serait quand même inchangé.
Le dividende serait 4858 et le diviseur un sous-multiple de 4858 plus grand que 1057.
Le premier quotient est inférieur à 4858/1057 donc à 6 et il divise 4858.
Il ne peut pas être 3 ni 4, ni 5, qui ne divisent pas 4858.
Si le quotient est 1, le diviseur est 4858/1 = 4858.
en première ligne : 5915 divisé par 4858 reste 1057
en deuxième ligne 4858 divisé par 1057 reste 630, au lieu de 315
Si le quotient est 2, le diviseur est 4858/2 = 2429
premier ligne : 5915 divisé par 2429 reste 1057
deuxième ligne : 2429 divisé par 1057 reste 315
troisième ligne : 1057 divisé par 315 reste 112
quatrième ligne : 315 divisé par 112 reste 91
cinquième ligne : 112 divisé par 91 reste 21
sixième ligne : 91 divisé par 21 reste 7
septième ligne : 21 divisé par 7 reste 0
le pgcd est le dernier reste non nul, ou, ce qui revient au même, le diviseur de la (dernière) division avec reste nul : 7
C'est la seule solution.
Dans ma troisième ligne : le quotient est inférieur à 5 (remplacer à 6 par à 5).
Dans la ligne suivante, 'ni 5' est inutile.


