bonsoir
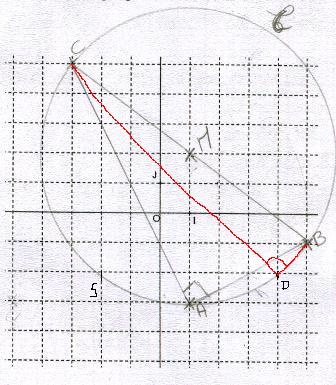
1)dans le repere orthonormal(O;I;J)ci contre placer les points A(1;-3) ,
B(5;-1) et C(-3;5)
2)démontrer que le triangle ABC est rectangle
3)a)déterminer par le calcul les coordonnées du point M centre du cercle circonscrit au triangle ABC.
b)quel est le rayon de ce cercle ? Justifier
4)démontrer que le point D(4;-2) est sur
5)calculer les coordonnées du point S symétrique de D par rapport à M
6)a)sans utiliser la réciproque du théorème de pythagore démontrer que le triangle DCB est rectangle en D
b)calculer l'arrondi au degré de la mesure de l'angle DCB

mes reponses:
2)AB²=(xb-xa)²+(yb-ya)²
     =(5-1)²+(-1-(-3))²
     =4²+2²
     =16+4
     =20 ul

AC²=(xc-xa)²+(yc-ya)²
   =(-3-1)²+(5-(-3))²
   =16+64
   80 ul

BC²=(xc-xb)²+(yc-yb)²
   =(-3-5)²+(5-1-1))²
   =(-8)²+6²
   =64+36
   =100 ul
AB²+AC²=20+80=100=BC²
donc AB²+AC²=BC²
d'apres la réciproque du théorème de pythagore on a ABCrectangle en A

3)a)calculer les coordonnées du milieu M du coté [CB]
    XM= xc+xb/2=-3+5/2=2/2= 1
    YM=xc+xb/2=5+(-1)/2=4/2= 2
    M(1;2)
b)aire du cercle de diamètre d=8,5cm
  aire du cercle C=(8,5:2)²*3,14
  aire du cercle C=56,71cm²
4)que faut il faire a cette question ??
5)M est le milieu [BC]
  XB=xm+xc/2=S=xm+(-5)/2
  YB=ym+yc/2=-1=ym+5/2
  5*2=(-5)+xm        10+5=xm
  -1*2=5+ym          -2-5=ym
10=-5+xm             xm=15
-2=5+ym              ym= -7
M(15;-7)
S est le milieu de [ac]
XC=xa=xs/2=-3=1+xs/2
YC=ya=ys/2=S=-3+ys/2
-3*2=1+xs         -6-1=xs
5*2=-3+ys         10+3=ys
-6=1+xs           xs=-7
10=-3+ys          ys=13
S=(-7;13)

6)a)besoin d aide ???
b)dans le triangle DCB rectangle en D
cos DCB=CB/CD
cosDCB=-3+5+5-1/-3+5+4-2
cosDCB=6/10
DCB=53°