Inscription / Connexion Nouveau Sujet
repére orthonormé
bonjour je suis nouveau sur se forum et j'aimerai avoir un peut aide concernant cette exercice
Soit un repere orthonormée(O,I,J) et les points A(-3;2),B(3;5),C(3;2.5).le triangle ABC est il rectangle? ou isocele?
J ai reuci a tracer le repere mais je ne c'est pas comment savoir si il est rectangle ou isocele. Merci de votre aide et bonne journée
Bonjour,
comment montrer qu'un triangle est rectangle ?
- Pythagore
- ou produit scalaire
- ou etc...
Comment montrer qu'un triangle est isocèle ?
par définition un tel triangle a deux côtés égaux
deux des distances AB, AC et BC sont elles égales ?
rebonjour
aucune distance n'est egale est en faisant le repere je me suis aperçu que se n'etait ni un triangle rectangle ni isocele que doit-je en conclure?
Que la réponse aux deux questions est "non" 
sauf erreur d'énoncé ou de recopie d'énoncé ou de calcul sur une question précédente qui donnerait les points ABC...
excuser moi car je me suis tromper c est bien un triangle isocele car AC=BC mais comment calculer AC et BC sachant que je n est que les points A(-3;2),B(3;5),C(3;2.5 et avec cela je dois determiner la longueur AC et BC comment doit je faire?
?????
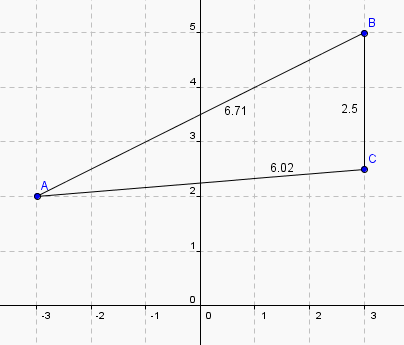
pour moi c'est bien un triangle tout ce qu'il y a de plus quelconque !
Quant à calculer la distance AB entre deux points A(x; y) et B(x'; y')
c'est une application directe du théorème de Pythagore :
d² = (x - x')² + (y - y')²
donc ici cela donne AB² = (3 - (-3))² + (5 - 2)² = 6² + 3² = 45 = 9*5 et donc AB = 3 5 = 6.7082... affiché 6.71 par Geogebra.
5 = 6.7082... affiché 6.71 par Geogebra.
je suis encore desoler mais pour C(3;-2.5) j ai mal lu mais ect ce qu on peut utiliser quand meme le theoreme de pythagore ou faut il un autre theoreme??
La formule que je t'ai donnée s'applique tout le temps.
Il faut juste faire bien attention aux signes comme dans mon 3 - (-3) = 6
Je te l'ai donnée la formule
la distance de deux points M de coordonnées (x; y) et N de coordonnées (x'; y') est
d² = MN² = (x - x')² + (y - y')²
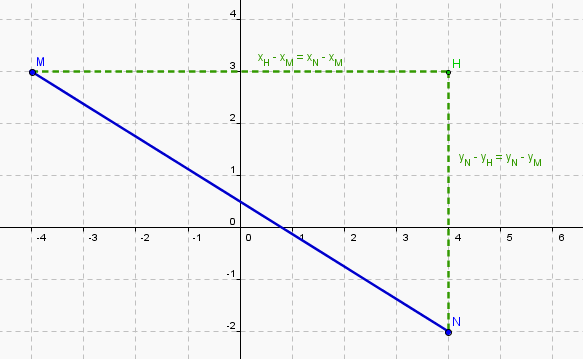
MH a pour longueur x - x' (sur la figure xN - xM)
NH a pour longueur y - y' (sur la figure yN - yM)
en valeur absolue, de toute façon (x - x')² = (x' - x)²
et Pythagore MN² = MH² + NH²
à mon avis cette formule est une formule de cours


