Inscription / Connexion Nouveau Sujet
repère orthonormé
Bonsoir
dans un repère orthonormé d'origne O on donne les points A (4;3) B (-1.5;2)
C est le symétrique de A par rapport à O
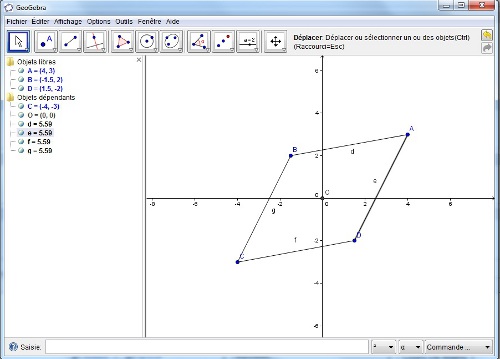
a) faire une figure
b) démontrer que les droites (OB) et (AC) sont perpendiculaires
c) démontrer les coordonnées du point D tel que le quadrilatère ABCD soit un losange
voilà j'ai un petit souci pour la question A comment puis je démontrer que deux droites sont perpendiculaires dans unr epère orthonormé SVP
Merci pour votre aide
bonjour
voilà j'ai un petit souci pour la question A comment puis je démontrer que deux droites sont perpendiculaires dans unr epère orthonormé SVP
le produit de leur coefficient directeur vaut -1
bonsoir
le professeur nous a donné un petit indice en disant qu'il fallait démontrer qu'il y a un triangle rectangle
je ne sais pas s'il faut que je démontre que AOB et BOC sont rectangle ?
merci
je ne sais pas s'il faut que je démontre que AOB et BOC sont rectangle ?
tu peux faire de cette facon
montrer que AOB est un triangle rectangle
On considère les points A(4;3) O(0;0) B(-1.5;2)
Calcul de AB
AB² = (xb-xa)²+(yb-ya)²
AB² = (-1.5-4)²+(2-3)²
AB² = (-5.5)²+(-1)²
AB² = 30.25 +1
AB² = 31.25
AB = 31.25
31.25
Calcul de OA
OA² = (xa-xo)²+(ya-yo)²
OA² = (4-0)²+(3-0)²
OA² = (4)²+(3)²
OA² = 16+9
OA² = 25
OA =  25
25
OA= 5
calcul de BO
BO² = (xo-xb)²+(yo-yb)²
BO² = (0-(-1.5))² + (0-2)²
BO² = (1.5)² +(-2)²
BO² = 2.25+4
BO² = 6.25
on a AB² = BO²+OA²
Donc d'après la réciproqque du théorème de Pythagore , AOB est un triangle rectangle en O
Montrer que COB est un triangle rectangle
On considère les points C (-4;-3) O (0;0) B (-1.5;2)
calcul de BC
BC ² = (xc-xb)²+(yc-yb)²
BC² = (-4-(-1.5))²+(-3-2)²
BC ² = (-4+1.5)² + (-5)²
BC² = (-2.5)² +25
BC² = 6.25+25
BC ² = 31.25
BC =  31.25
31.25
calcul de OB
OB ² = (xb-xo)²+(yb-yo)²
OB² = (-1.5-0)²+(2-0)²
OB² = (-1.5)²+(2)²
OB² = 2.25+4
OB² = 6.25
OB =  6.25
6.25
calcul de CO
CO² = (xo-xc)²+(yo-yc)²
CO² = (0-(-4))²+(0-(-3))²
CO² = (4)² + (3)²
CO² = 16+9
CO²= 25
CO = 25
25
CO =5
On a BC² = CO² +OB²
Donc d'après la réciproque du théorème de Pythagore, COB est un triangle rectangle en 0
Comme j'ai démontré que les deux triangles sont rectangles
Pour pouvoir répondre à la question b : démontrer que (OB) et (AC) sont perpendiculaires
que dois je dire ?
Est ce que si je dis
comme les triangles AOB et COB sont des triangles rectangles alors les droites (OB ) et (AC) sont perpendiculaires ?
Merci
pour la question c
Si ABCD est un parallélogramme alors ses diagonales ont les mm milieu donc O doit être le milieu de [BD]
On considère les points O (0;0) B (-1.5;2) D ?
xo = xb+xd/2
0=-1.5+xd/2
0*2/2 = -1.5 + xd/2
0 = -1.5 + xd
xd = 1.5
yo = yb+yd/2
o = 2 +yd/2
0*2/2 = 2 + yd/2
0 = 2 + yd
yd = -2
donc D (1.5;-2)
montrer que ABCD est un losange
Calculer AB
AB² =(xb-xa)²+(yb-ya)²
AB² = (-1.5 - 4)² + (2-3)²
AB² = (-5.5)² +(-1)²
AB² = 30.25 + 1
AB² = 31.25
AB = 31.25
31.25
calculer BC
BC ²= (xc-xb)²+(yc-yb)²
BC² = (-4-(-1.5))²+(-3-2)²
BC² = (-4+1.5)² +(-5)²
BC² = (-2.5)² +25
BC² =6.25+25
BC² =31.25
BC = 31.25
31.25
Les côtés [AB] ET [BC] du parallélogramme ABCD sont égaux donc ABCD est un losange
en fait on veut juste trouver les coordonnées de D
c) démontrer les coordonnées du point D tel que le quadrilatère ABCD soit un losange
oui il faut trouver les coordonnées de D
et en conclusion j'ai voulu montrer que c'était bien un losange