Inscription / Connexion Nouveau Sujet
Repère orthonormé
Bonjour, je suis élève de Seconde, j'ai un devoir à rendre lundi en mathématiques, mais je suis bloquée.
Dans ces questions, on doit utiliser géogébra.
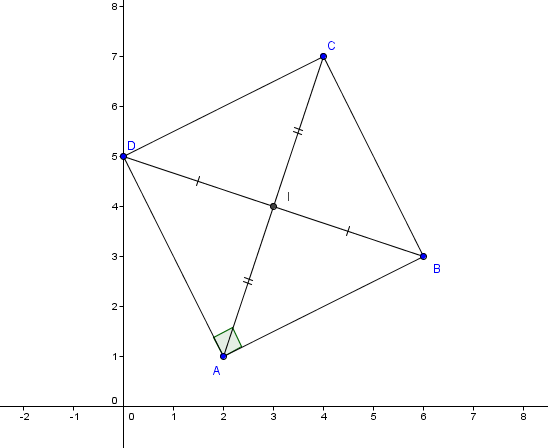
-> Dans un repère orthonormé, on considère les points A(2;1), B(6;3) et C(4;7).
1) faire une figure et compléter au fur et à mesure.
2) déterminer les coordonnées du milieu I de [AC].
3) on appelle D le symétrique de B par rapport à I. Déterminer les coordonées de D.
Jusqu'ici, j'y arrive...
4) quelle est la nature du quadrilatère ABCD?
5) en déduire que le point B appartient au cercle (C) de diamètre [AC]
6) a- faire une figure avec l'aide d'un logiciel de géométrie dynamique (géogébra)
b- conjecturer la position du point M
c- on appelle x l'abscisse du point M
démontrer que (BM) est une tangente au cercle (C)
si et seulement si x est une solution de l'équation 10+ (6-x)2 +9 = (3-x)2 +16
d- résoudre l'équation précédente. CONCLURE.
Merci de votre aide ! 
Bonjour Madatance et Leile
comme je ne conçois pas un problème de géométrie sans figure j'en ai réalisé une
je vous laisse poursuivre l'aide
merci Hekla pour cette figure,
j'attendais la réponse de Madatance (la figure donne la réponse aux questions..)
à Madatance : dis moi ce que tu trouves comme coordonnées pour I et D,
puis pour répondre a la question 4) tu peux calculer des distances (par exemple AC, BD, CD, CB, ...)
Enfin, complète ton énoncé : il manque le a) de la question 6 : on ne sait pas comment se place M.
Merci pour la figure,
désolée, pour le a- on veut déterminer M, point de l'axe des abscisses tel que (MB) soit tangente au cercle (C)
I= (3;4)
D= (0;5)
OK pour I et D.
ABCD est un //ogramme (ses diagonales se coupent en leurs milieux)
si tu parviens à montrer qu'elles sont de meme longueur, tu pourras dire que c'est un rectangle, puis en calculant 2 cotes consecutifs, dire que c'est un carré..
ou si tu calcules les distances BD, AD et AB par exemple, tu pourras dire avec pythagore que le triangle ABD est rectangle en A et meme qu'il est isocèle..
et en déduire la nature de ABCD.
Vas y !
Voilà, j'en ai fini avec la question 4, effectivement, j'ai calculé les distances, pour montrer que ABCD est un rectangle, puis un carré.
Pour la question 5,
propriété: si les trois sommets d'un triangle (ici, ABC, rectangle en B) sont sur un même cercle, alors on dit que le
triangle est inscrit dans ce cercle. On peut aussi dire que le cercle est circonscrit à ce triangle.
Pour la question 6,
b- On peut conjecturer que le point M(5;0)
C'est vraiment pour les dernières questions où je ne sais pas du tout comment faire...
Merci beaucoup de votre aide!
question 5 : tu ne prouves pas que B est sur le cercle...
puisque ABCD est un carré, le triangle ACB est rectangle en B.
il est inscrit dans un cercle dont un diamètre est l'hypoténuse du triangle
==> il est inscrit dans le cercle de diamètre AC
donc B est sur ce cercle.
6)
si (MB) est tangente au cercle en B,
alors IB est perpendiculaire à MB, et le triangle IBM est rectangle en B.
d'après pythagore, on aura alors IM² = IB² + BM²
pose M(x;0), calcule IM², calcule IB² et BM² ..
qu'est ec que tu trouves ?
Ok pour la question 5 
Pour la 6,
IM2 = x2-6x+25
IB2 = 10
BM2 = x2-6x-6x+36
Voilà 
Je vais faire mes calculs, et ensuite je vous tiens au courant !
En fait, je pense que je me suis trompée dans mes calculs....
Le problème, c'est que je n'arrive pas à comprendre pourquoi on fait cela, donc je n'arrive pas à répondre...
Quel est le but de cette équation?
IB² = 10
BM² = (x-6)²+9
IM² = (x-3)² + 16
et la question est : démontrer que (BM) est une tangente au cercle (C)
si et seulement si x est une solution de l'équation 10+ (6-x)² +9 = (3-x)² +16
tu y es, non ?
ensuite, tu peux développer pour résoudre et trouver x
pourquoi on fait ça :
MB est tangente au cercle en B si et seulement si IB² + BM² = IM²
ce qui revient à l'équation en question.
OK ?
Bonsoir, je suis désolée, je n'ai pas terminé, je vais essayer de résoudre cette équation, merci de votre patience 
Je me reconnecte demain.... pourriez-vous m'aider de nouveau, je vais essayer de terminer cela ce soir!
je te donne le début :
10+ (6-x)² +9 = (3-x)² +16
10 + (36 - 12x + x²) + 9 = (9 - 6x + x²) + 16
continue pour trouver x
c'est presque fini.
je serai là demain..
Je viens de commencer à résoudre l'équation,
cela me donne:
(3x)2 + 16 = 10+ (6-x)2 +9
=> x2 - 6x + 25= 10+ x2 - 12x + 45
=> x2- 6x= x2 - 12x+ 30
Maintenant, que dois-je faire?
Je ne sais pas comment faire quand il y a x2 dans une équation....
parfait !
Ca confirme ta conjecture : pour que (MB) soit tangente au cercle, il faut placer M sur l'axe des abcisses en (5;0).



