Bonjour

On donne dans un repère (O;I;J) les points A (-6;-6) B(-2;6) C(10;7)

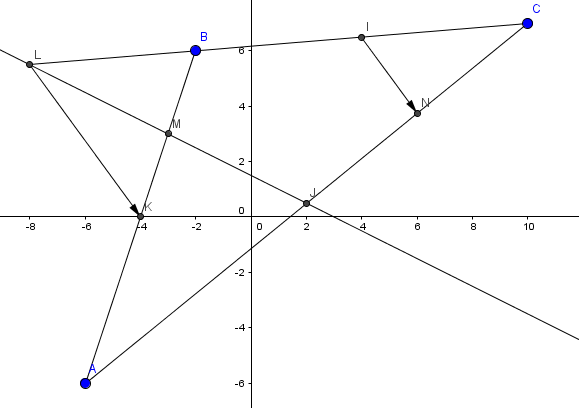
1. Construire la figure que l'on complétera au fur et à mesure

2. Déterminer les coordonnées des points I,J,K milieux respectifs de [BC],[CA],[AB]

3. Déterminer les coordonnées de L symétrique de I par rapport àB

4. Déterminer les coordonnées de M et N milieux respectifs de [BK] et [CJ]

5. Montrer que les droites (IN) et (LK) sont //

6. Montrer que les points L,M,J sont alignés


mes réponses

1. I milieu de [BC]

I = (xb+xc/2;yb+yc/2)

I = (-2+10/2; 6+7/2) = (8/2 ; 13/2) = (4;6.5)

I (4;6.5)

J milieu de [CA]

J =(xc+xa/2 ;yc+ya/2) = 10+(-6)/2; 7+(-6)) = (10-6/2 ; 7-6/2) =(4/2; 1/2) = (2;0.5)

J (2;0.5)

K milieu de [AB]

K=(xa+xb/2;ya+yb/2) =(-6+(-2); -6+6/2) = (-6-2/2;0/2) = (-8/2;0) =(-4;0)

K (-4;0)

2. Si un point L est la symétrique d'un point I par rapport à B alors B est le milieu du segment  [LI]

xb= xl +xi/2
-2 = xl +4/2
-4/2 = xl +4/2
-4 = xl +4
-4-4 = xl
xl = -8

yb = yl + yi/2
6=yl+6.5/2
12/2=yl+6.5/2
12=yl+6.5
12-6.5=yl
yl =5.5

L(-8;5.5)

4. M milieu de [BK]

M=(xb+xk/2;yb+yk/2)

M=(-2+(-4)/2; 6+0/2)
M= (-2-4/2 ; 6/2) = (-6/2;3) =(-3;3)

M(-3;3)

N milieu de [CJ]

N= (xc+xj/2;yc+yj/2)

N= (10+2/2; 7+0.5/2) = 12/2; 7.5/2) = (6;3.75)

N (6;3.75)

5. cordonnées de IN

IN (xi-xn;yi-yn)
IN (4-6;6.5-3.75)
IN(-2;2.75)

coordonnées de LK

LK (xl-xk;yl-yk)

LK(-8-(-4); -5.5-0) LK(-4;5.5/2) LK (-2;2.75)

donc IN = LK

Donc (IN)//(LK)

6. calcul du coef directeur de la droite (LM)

m= ym-yl/xm-xl

m= 3-5.5/-3-(-8) = -2.5/5 = -0.5

calcul du coef directeur de la droite (LJ)

m' =yj-yl/xj-xl = 0.5-5.5/2-(-8) = -5/10 = -0.5

m = m' = -0.5 donc les points LMJ sont alignés

merci pour les personnes qui voudront bien me corriger

merci