Inscription / Connexion Nouveau Sujet
Résolution algébrique d'une équation.
Bonjour à tous,
Donc j'ai un petit problème pour résoudre une équation.
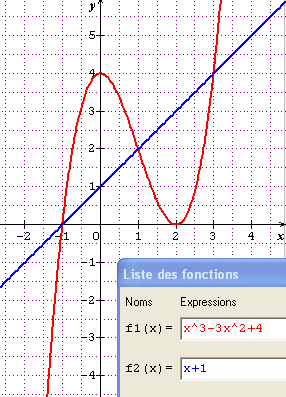
f(x)=x^3-3x²+4 et g(x)=x+1En déduire la résolution algébrique de l'équation f(x)=g(x)
pour info ===> x^3-3x²+4=(x-2)²(x+1)
J'ai fait (x-2)²(x+1)=x+1et je trouve x=2 alors que je devrais trouver 2 solutions
S={2;-1} ( résolution graphique )
excusez-moi je me suis tromper dans l'énoncé, je devrais trouver S={-1;1;3} c'est ce que j'ai trouver avec la résolution graphique.
merci
Je ne vois pas où tu veux en venir ?
il me faut la résoution algébrique, la résolution graphique je sais que c'est s={-1;1;3}
De l'utilité de poster un énoncé clair, complet et exact suivi des réponses apportées.
J'ai cru que tu avais fini. Et je n'ai pas voulu que le topic reste rouge pour ne pas faire perdre leur temps aux correcteurs.
____________________________________
Et alors, que proposes-tu pour la résolution algébrique ?

Rechercher les solutions c'est chercher les valeurs de x pour lesquelles :
(x - 2)2 (x + 1) = (x + 1)
1) Si x  -1 alors...
-1 alors...
2) Si x = -1 alors...

Non, en effet, ce n'est pas "normal". Et je ne vois pas comment tu trouves x = 2
Peux-tu poster ton raisonnement et tes calculs ?

oui bien sur donc:
(x-2)²(x+1=(x+1)
(x-2)(x-2)[x+1)-(x+1)]=0
(x-2)(x+1-x-1)=0
x-2=0
x=2
je sais qu'il doit y avoir une erreur dans mon calcul mais je ne sais pas où.
La factorisation est fausse.
(x - 2)2 (x + 1) = (x + 1)
(x - 2)2 (x + 1) - (x + 1) = 0
Quel est l'expression qui peut être mise en facteur ? Que devient cette équation une fois le premier membre factorisé ?

Oui, c'est l'une des trois solutions...
mais il faut aussi calculer les deux autres solutions de l'équation !