Inscription / Connexion Nouveau Sujet
Résolution d'Equation
Bonjour à tous,
j'ai un petit problème, je ne me souviens plus comment résoudre ces équations :
cos x  -1
-1
1/2  sin x
sin x  (
( 3)/2
3)/2
- ( 2)/2 < cos x < 1/2
2)/2 < cos x < 1/2
sin²x  1/2
1/2
Voilà merci d'avance pour votre aide
Bonjour,
la première est une question de cours.
Pour la seconde, il suffit de résoudre les équations
sin(x)=1/2
sin(x)=racine de 3/2
et de voir comment varie le sinus.
Idem pour les deux suivantes.
Que voulez vous dire par "une question de cours" ?
Merci de l'aide je vais essayer je vous dirais ce que je trouve
Par exemple pour la deuxième :
1/2  sin x
sin x  (
( 3)/2
3)/2
sin x = 1/2  sin x
sin x  sin x = (
sin x = ( 3)/2
3)/2
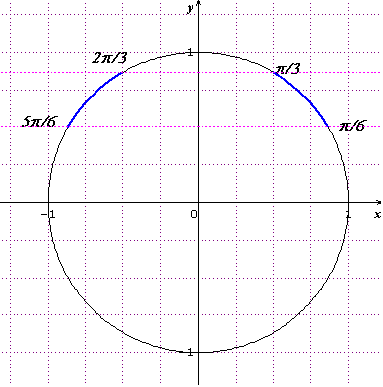
5 /6
/6  sin x
sin x 
 /3
/3
C'est ça ???
Pour la première question cos x -1, tu dois savoir que, pour tout réel x on a -1
-1, tu dois savoir que, pour tout réel x on a -1 cos x
cos x 1
1
Pour la seconde question, il faut utiliser le cercle trigonométrique. Tu en déduis que l'ensemble des solutions est S=
Oui je sais me servir du cercle mais je dois les résoudre ces équations et non pas les déduire à partir du cercle
Alors, si tu dois "résoudre" de façon purement algébrique, c'est beaucoup plus long à rédiger :
l'inégalite 1/2 sin x
sin x
équivaut à (sur l'intervalle [0 ; 2pi[ )
ou
il faut alors se servir du sens de variation de la fonction sinus et conclure ...
Mais, encore une fois, en tant que professeur ayant souvent enseigné en 1S et en TS, je préfère mille fois qu'un élève se serve directement de son cercle trigonométrique ... et comprenne bien ce qu'il fait.
Oui, la seule solution est pi (sur l'intervalle [0; 2pi[) car l'équation cos x=-1 a pour seule solution x=pi. Donc, sur R l'ensemble des solutions de l'inéquation cos x -1 est l'ensemble des réels de la forme pi+2kpi où k est un entier relatif ...
-1 est l'ensemble des réels de la forme pi+2kpi où k est un entier relatif ...
Ok merci et pour la 2ème vous n'auriez pas plus simple à part le cercle trigo et le sens de variation?
Par conséquent les solutions sont:
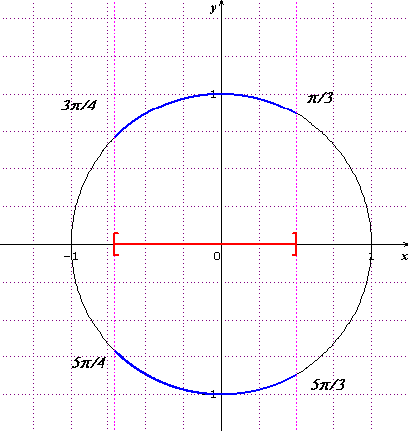
[pi/3 ; 3pi/4 ] U [5pi/4 ; 5pi/3]
??
et pour la dernière ? car avec le carré je ne vois vraiment pas comment faire
Pour la 3ème j'ai pas le droit de dire :
- 2 /2 < cos x < 1/2
2 /2 < cos x < 1/2
cos 3pi/4 < cos x < cos pi/3 OU cos 5pi/4 < cos x < cos 5pi/3
DONC : x [pi/3, 3pi/4] U [5pi/4, 5pi/3]
???
Oui j'avais oublié de préciser que je travaillais uniquement sur cet intervalle. Par contre la dernière reste un mystère pour moi
Pour la 2, je peux appliquer le même raisonnement que j'ai utilisé à la 3. donc il me reste juste la dernière
L'inéquation a2
équivaut à a2-
 0
0
autrement dit (a-)(a+
)
 0
0
autrement dit (a-)(a+
)
 0
0
autrement dit (a-)(a+
)
 0
0
En faisant un tableau de signes, on arrive à a
Il suffit alors de remplacer a par sin x ...