- Ensemble et application Partie II
- Équations différentielles : un Cours complet avec des exemples
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Un best-of d'exos de probabilités (après le bac)
Inscription / Connexion Nouveau Sujet
Resolution d'un triangle
Bonjour à tous.
Voilà j'ai un exercice à faire et je bloque complètements :
Avec ses éléments je n'arrive que à calculer AB.
Quelqu'un pourrait m'aider svp.
Merci d'avance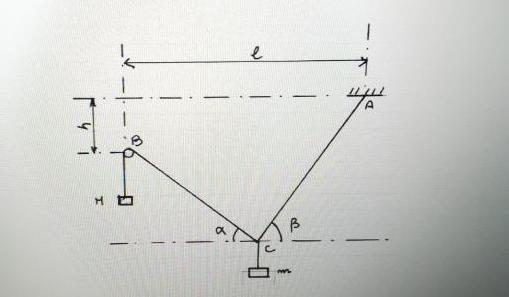
***image recadrée sur la figure, les scans de sujets ne sont pas autorisés***![]() Sujet ancien- ne plus donner ce lien-merci
Sujet ancien- ne plus donner ce lien-merci
Bonjour,
Appelle D et E les projections de A et B sur l'horizontale passant par C.
Considère les triangles ACD et BCE, écris :
cos( ) = ...
) = ...
sin( ) = ...
) = ...
cos( ) = ...
) = ...
sin( )= ...
)= ...
EC + CD = l
AD - BE = h
Tu devrais avoir assez de relations pour aboutir.
Merci pour ta réactivité LeHibou,
Je vais essayer ce soir et je reviendrai sur le sujet si nécessaire.
ruitopo, si tu avais lu le règlement, tu aurais vu que les scans de sujets ne sont pas autorisés...merci de recopier désormais ton énoncé, suite à mon message, afin que ce sujet ne perde pas son intérêt
(modérateur)
Désolé, voici l'énoncé :
Une masse m est suspendue à l'extrémité de deux fils inextensibles AC et BC . Le fil AC
est relié au point fixe A . Le fil BC passe sur la poulie B et supporte une masse M . La
distance horizontale entre A et B est l et la distance verticale entre A et B est h.
La position du point C est définie par l'angle alpha entre CB et l'horizontale. On appelle Tca la tension du fil AC et beta l'angle entre CA et l'horizontale.
Question: Exprimer les longueurs AC et BC en fonction de l , h , alpha et beta .
OK, donc j'obtiens 2 triangles rectangles. Mais ne dois-je pas connaitre au moins un coté pour pouvoir exprimer les longueurs de AC et BC?
Merci d'avance
Bonjour,
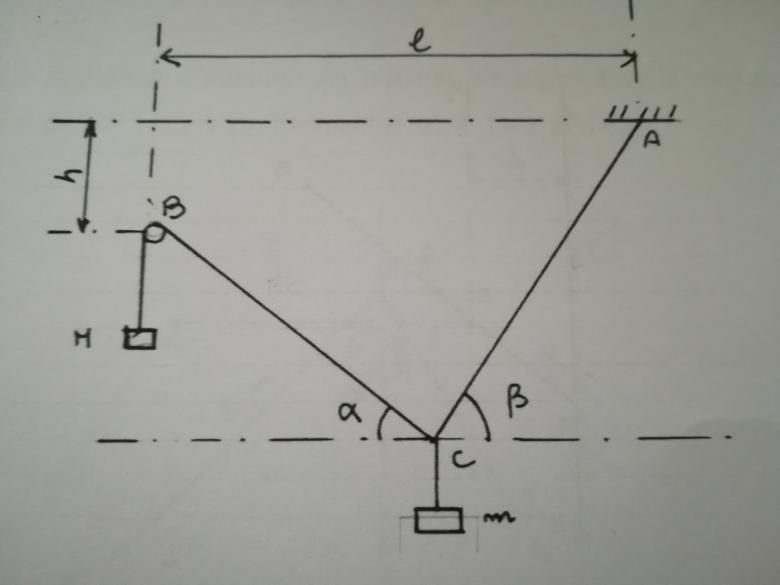
Je dois exprimer la relation vectorielle qui traduit l'équilibre du système si dessous.
Je suis complètements perdu, je ne sais mémé pas par ou commencer.
Quelqu'un pourrais m'aider svp.
Merci d'avance
*** message déplacé ***
inscrit de la journée....image non conforme, et maintenant multipost...heureusement que j'avais mis le lien des règles à respecter en début de journée....


Bonsoir,
calcul de BC et AC
cela revient à résoudre un système de 2 équations à 2 inconnues BC et AC.
Bonjour,
Donc pour BC cos (alpha) + AC cos (beta) = l , je dois m'en servir pour aboutir a BC ?
Puis remplacer le résultat de BC dans la deuxième équation pour aboutir a AC?
Je suis vraiment désolé, mais pour être honnête je ne comprends rien, le faite de ne pas avoir des chiffres me perturbe.
Quelqu'un pourrait m'éclaircir sur ce sujet?
Merci d'avance
Bonjour,
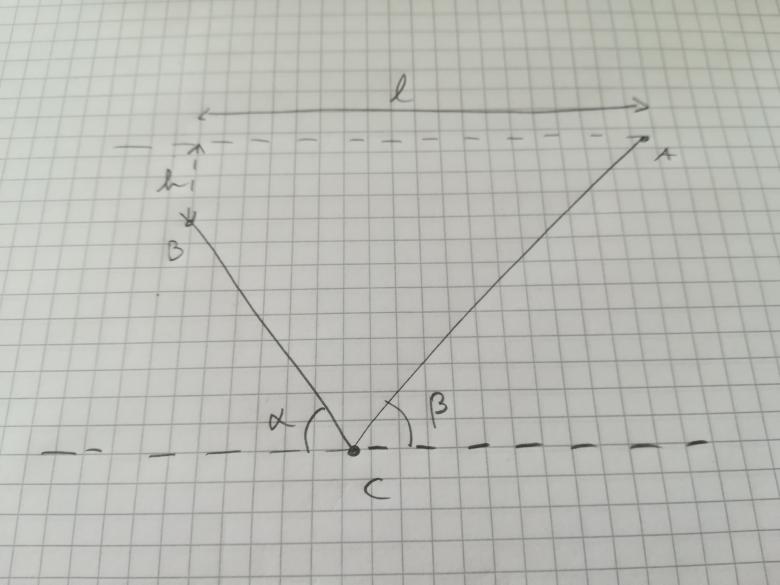
Je bloque sur cette exercice :
Exprimer les longueurs AC et BC en fonction de l , h , alpha et beta.
Je commence par projeter la relation vectorielle BA=BC+CA sur l'horizontale et sur la verticale
J'arrive donc a :
l=BCcos(alpha)+CAcos(beta)
h=-BCsin(alpha) +CAsin(Beta)
Apres le neant complet.
Quelquen pourai m'aider svp?
Merci d'avance
*** message déplacé ***
Il s'agit maintenant de résoudre le système de deux équations à deux inconnues (BC et CA) que tu as écrit.
*** message déplacé ***
Donc pour BC cos (alpha) + AC cos (beta) = l , je dois m'en servir pour aboutir a BC ?
Puis remplacer le résultat de BC dans la deuxième équation pour aboutir a AC?
Je suis vraiment désolé, mais pour être honnête je ne comprends rien, le faite de ne pas avoir des chiffres me perturbe.
Quelqu'un pourrait m'éclaircir sur ce sujet?
Merci d'avance
*** message déplacé ***
multicompte (rien que 3 comptes actuellement...), multipost...

 extrait de
extrait de Q24 - Moi, tout ce qui m'intéresse, c'est d'obtenir de l'aide. Vos règles du forum, je n'en ai rien à faire !
donc deux comptes à fermer si tu veux pouvoir revenir un jour...


 trigonométrie en post-bac
trigonométrie en post-bac