Inscription / Connexion Nouveau Sujet
SABCD une pyramide régulière et la base est le carré de côté 2a
Bonjour à tous
Soit SABCD une pyramide régulière dont la base est le carré de côté 2a et dont les faces latérales sont des triangles isocèles d'angles au sommet de mesure 30°.
On désigne respectivement par I, J et H le milieu de [AB], le milieu de [CD] et le centre du carré ABCD.
Déterminer, en fonction de a, la hauteur SH de cette pyramide.
Je sais que la correction de cet exercice est proposée mais dans cette correction un intègre un point K qui ne fait pas partie de l'exercice et avec ce point K je ne comprends rien.
N'y a t'il pas un autre moyen pour calculer la hauteur SH?
Merci d'avance
Bonsoir eurovia
Je peux te proposer une autre méthode, mais elle nécessite la connaissance du sinus d'un angle aigu dans un triangle rectangle... ("sinus = côté opposé/hypoténuse")
Voici une figure.
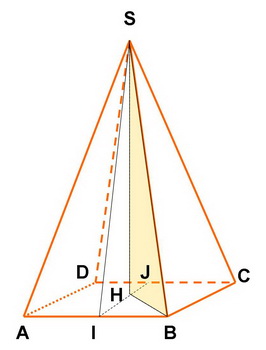
L'idée est de trouver SH dans le triangle rectangle SHB.
Tu peux trouver HB (hypoténuse du triangle rectangle HIB) et SB (hypoténuse du triangle rectangle SIB que tu trouveras en calculant ))
Re hiphigenie
J'ai honte d'avouer ma nullité en maths et c'est dire que je rame vraiment mais pourtant j'essaye....donc ta méthode proposée, je n'y arrive pas. J'ai essayé autre chose et je bloque...
Peux tu me dire si le début est correct....j'y suis depuis hier et aujourd'hui et je t'assure que je rame... et je n'arrive pas à réduire
Sachant qu'un carré a ses diagonales de mêmes longueurs, qui se coupent en leur milieu et qui sont perpendiculaires.
Je me met dans le triangle ABC rectangle en B
Le théorème de Pythagore donne :
CA² = AB² + CB²
CA² = 2a² + 2a²
CA² = 4a²
CA = √4a²= 2√2a²
Je sais que AH est la moitié de CA donc, 2√2a² / 2 = 1√2a²
Donc, AH = 1√2a²
Dans le triangle AHS rectangle en H Le théorème de Pythagore donne :
AS² = AH² + SH²
SH² = AS² - AH²
Sachant que c'est un triangle équilatéral AS = AB = 2a
Donc
SH² = 2a² - (1√2a²)²
et là, je bloque..... HELP
Il y a quelques erreurs...
CA² = AB² + CB²
CA² = 2a² + 2a²
CA² = 4a²
CA = √4a²= 2√2a²
Je sais que AH est la moitié de CA donc, 2√2a² / 2 = 1√2a²
Donc, AH = 1√2a²
Donc,
Sachant que c'est un triangle équilatéral AS = AB = 2a
Ils ne sont pas équilatéraux

Par conséquent, la fin de ta résolution n'est plus correcte.
D'ailleurs l'énoncé dit ceci :
les faces latérales sont des triangles isocèles d'angles au sommet de mesure 30°.
Bonjour,
une des faces en vraie grandeur :
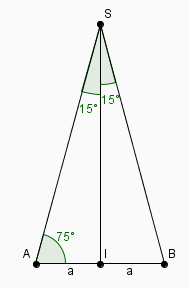
on obtient : a = SI.tan(15°) d'où SI = a/tan(15°)
mais 15° ne fait pas partie des "angles remarquables" dont les valeurs trigonométriques sont connues.
pour obtenir que tan(15°) = 2 -  3 il faut faire quelques acrobaties en calculant l'aire de ce triangle par des moyens détournés ...
3 il faut faire quelques acrobaties en calculant l'aire de ce triangle par des moyens détournés ...
(ou résoudre l'équation de la tangente d'un arc moitié, qui n'est pas du niveau AMHA)
donc : calculette pour tan(15°), je ne vois que ça ici dans l'immédiat.
ou laisser de façon "littérale" "tan(15°)" comme ça.
ce calcul donne ensuite directement la hauteur de la pyramide via Pythagore dans le triangle SHI de la 1ere figure d'Hiphigenie
Vraiment merci à vous tous mais rien à faire
Merci vraiment à toi hyphigenie et mathafou mais vous avez la passion des maths ça se voit....et moi, je suis dingue de français et d'histoire/géo!!!!!
Pour hyphigenie, j'en suis (depuis ton dernier message) à rien :
Voilà ce que j'ai fait :
AH = √2a
Dans le triangle AHS rectangle en H le théorème de Pythagore donne :
AS² = HS² + HA²
Sachant que c'est un triangle isocèle AS = AHx√2 = √2a x √2
Donc
SH² = AS² - AH²
SH² = (√2a x √2)²-(√2a)²
SH = ??????
Sachant que c'est un triangle isocèle AS = AHx√2
quel triangle est isocèle ? AHS ? non ! il est juste rectangle et c'est tout.
en vraie grandeur en dépliant à plat comme pour un patron :
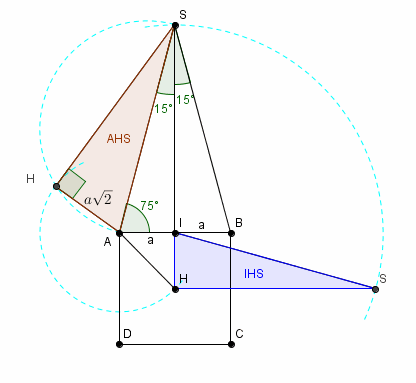
les triangles rectangles IHS et AHS
AS est très loin d'être AH√2 !!
(AH√2 = AB)
Sincèrement désolé mais je ne comprends rien.
Donc, le fait d'avoir trouvé AH ne m'aide pas ou alors je ne vois pas
Merci en tout cas de votre patience et votre gentillesse.
Passez un bon dimanche (certainement meilleur que le mien.....)
Merci encore beaucoup
Le calcul du sinus ou de la tangente de l'angle de 15° est ici incontournable.
la méthode d'Hiphigénie calcule AS = AI/sin(15°) et alors oui, avec AS et AH on obtient SH
ma méthode calcule SI = AI/tan(15°) et alors c'est le triangle SHI qui donne SH
Ton "corrigé" semblait faire intervenir un mystèrieux point K.
Peux tu en dire plus là dessus ?
là est peut être "planqué" le calcul des sinus ou tangente 15° !
sinon pour calculer ça exactement, comme je le signalais, il faut faire intervenir le calcul détourné de l'aire de ABS, c'est un peu compliqué !
Avec d'autres notations, et cela pourait parfaitement faire l'objet d'un exercice entier à part, ça s'est d'ailleurs déja vu ici cet exercice là :
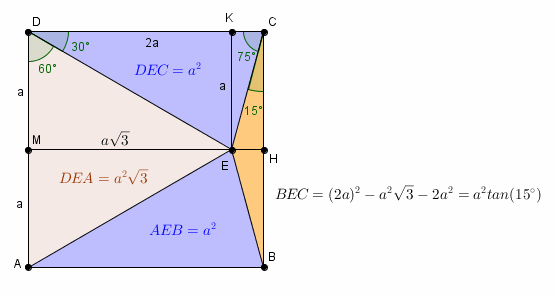
dans un carré de côté 2a, on trace un triangle équilatéral ADE
les divers angles sont alors obtenus facilement (DE=DA=DC, DEC est isocèle, donc l'angle à la base = (180 - 30)/2 = 75)
La hauteur ME est et donc l'aire de ADE est
l'aire des triangles DEC et AEB de bases 2a et de hauteur a est directement
il reste donc l'aire de BEC = l'aire du carré moins celle des triangles ADE, DEC et BEC
aire BEC =
mais cette aire est aussi !
on en tire
ce qui pour revenir à nos notations à nous dans notre triangle ABC :
une fois obtenu ça (mais à mon avis ces calculs ne sont pas du niveau, tout au moins sans "guide" explicite étape par étape dans un énoncé de problème complet)
une fois obtenu ça donc, la suite est "facile" :
A voir si le fameux point K simplifie ça ...
Mathafou :
La réponse est donnée sur ce même site : https://www.ilemaths.net/maths_2_espace01_4exos-correction.php
mais il y un point k qui sort de nul part.
Si j'étais pas motivé, je recopierais la correction sans rien y comprendre mais ce n'est pas mon style même si je suis plus que nul en maths.
cet exo est une torture pour moi et j'essaye vraiment de rechercher dans mes cours et mes livres mais avec des lacunes, seul, c'est pas facile.
Ma mère veut payer un étudiant pour me donner des cours...et je crois qu'elle a raison!
Vu,
effectivement on n'a pas besoin avec cette méthode de calculer explicitement les tangentes et sinus de 15° !
c'est même parfaitement clair, si la figure était "réaliste" ça aiderait encore mieux !!
je remets ici :
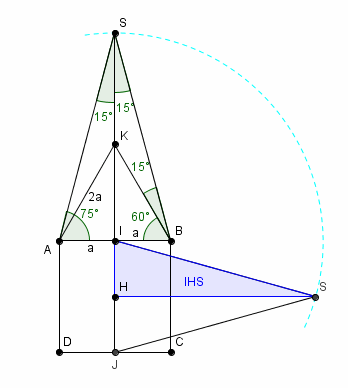
j'ai repris mes "rabattements" en vraie grandeur.
Ajouter des points dans une figure est une pratique courante !
(on ne peut pas faire grand chose en géométrie si on ne prend pas ce genre d'initiative !)
donc ici on ajoute un point K qui va nous aider, et ce point K on le choisit pour que ABK soit équilatéral. Bien sûr l'idée de "créer" ainsi ce triangle équilatéral, c'est un peu du génie ! il semble douteux qu'on puisse le "deviner" sans y être incité... on est d'accord.
Donc ses côtés sont égaux AK = KB = AB = 2a
et ses angles font tous 60°
On a calculé depuis longtemps déja que le triangle ABS isocèle et angle en S = 30° = 2x15° (dans un triangle isocèle la médiane SI est hauteur et bisectrice)
et que angle à la base de ce triangle ABS est SAB = SBA = (180 - 30)/2 = 75°
ceci donne tous les angles marqués sur la figure.
Intéressons nous aux longueurs maintenant
SI que l'on cherche sera SK + KI
SK est la hauteur du triangle équilatéral, et s'obtient par Pythagore dans IBK (ou AIK)
les angles de 15° dans le triangle KBS prouvent que ce triangle est donc isocèle.
Par conséquent KS = KB = 2a
et voila comment on obtient le que je citais dans mon dernier post, mais de façon beaucoup plus simple.
la suite est comme je disais : dans IHS, IH² = IS² - HI² etc.
Merci merci beaucoup mathafou
Je ne savais vraiment pas que prendre un point k (dans l'exemple) était autorisé voir très courant.
Avec votre dessin (et non celui mis dans la correction), je visionne beaucoup mieux la situation.
Vraiment merci pour vos explications qui sont beaucoup plus claires (en tout cas pour moi!).
Je vais approcher cet exo plus clairement.
Merci de votre temps passé pour vos explications (surtout un dimanche!). Je suis en admiration devant vous qui avez des connaissances et un savoir matheux. Si je pouvais avoir les mêmes facilités.....je suis jaloux (je rigole).
MERCI MERCI MERCI
La 2nde générale est très dure pour moi en maths!



