svp j'aurais vraiment besoin que quelqu'un m'aide
c'est urgent pour mon projet
je remercie d'avance la personne qui pourra m'aider

Bonjour Elvadria ,
Il faut x+y<1 .

(en supposant AB=1).

Explication :Soit M' sur AB telque MM'//BC :pour que M soit dans ABD ,il faut AM'<AB ,or AM'=x+y >>> x+y<AB.  

Pour que M soit dans ABC , pas ABD .Jesuis mal réveillé!

Bonjour,
>> Rolands
je crois qu'il y a un probleme dans ton post, car peut importe où est le point DANS le carré, on a AM'<AB...

Tu m'étonnes , Tomm-bou , Si M est au dessus de BC la // à BC menée par M coupe AB au delà de B donc AM'>AB ou x+y>AB . Es-tu d'accord ?

on va se faire un dessin parce que je suis embrouillé !
on est d'accord, un carré ABCD. les diagonales sont (AC) et (BD).
on veut savoir dans quel triangle rectangle est le point M en fonction de ses coordonnées.
tu proposes de tracer la droite MM' parallele a BC, ce que j'ai fait.
et ici, peut importe ou est le point M dans le carré, on a AM'<AB...
Tomm-Bou

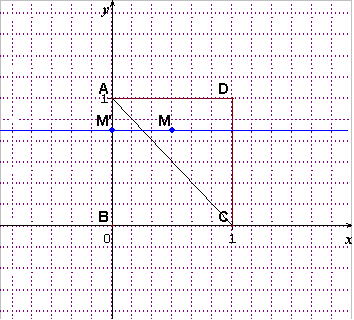
Erreur dès le début : le carré s'appelle ABDC et non ABCD sinon on n'a pas ABC rectangle en A et BCD rectangle en D ...

En effet , nous n'avons pas la même figure;
j'ai pris A à l'origine des axes , B sur l'axe des abscisses et C sur celui des ordonnées : le point D en découle .
Veux-tu t'adapter à mon dessin ou l'inverse ?

ok je suis desole c moi qui me suis trompe dans les coordonnées
mais en fait je voulais savoir si c'etait dans l'un ou dans l'autre des triangles. Donc le carré est bien ABDC

Voila ce que j'ai trouve :
Soit tel que soit orthogonale a l'hypothenuse de ABC, c'est a dire BC.
Calculons le signe de scalaire (vect BA).
Si scalaire(BM) est de meme signe que le dernier
scalaire alors M est dans ABC, sinon il est dans BCD.

Est ce que c'est correct ?

Je comprends mal ce que tu veux exprimer :
"si U.BM est de même signe que le dernier"???
U peut être le vecteur (1;1).  U.AM=x+y , ensuite ???
essaie plutôt de comprendre l'explication que j'ai donnée .
Bonsoir Elvadrias et Tomm .

Re tout le monde !
>> rolands
ok, la je comprends. (Cf. Dessin joint). Cette histoire d'ordre des points, j'avais pas remarqué.
ce petit probleme était... interessant !

bon, j'y vais, une journée de cours qui m'attend
a+
Tomm-Bou :d

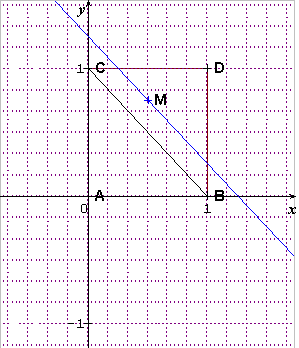
Très bien ,
maintenant j'aimerais que,à ton tour , tu m'expliques en détail comment tu fais pour envoyer un croquis .
Je ne te répondrai qu'à mon retour pour te dire si j'y arrive , car je vais m'absenter 8 jours.
Merci , et à bientôt .

En fait je suis a peu pres sur de ma supposition et ca se voit bien sur le dessin
Soit u est un vecteur orthogonal a BC, calculons u.BA
Maintenant calculons u.BM.
Si u.BA est de meme signe que u.BM alors M est dans le triangle ABC.


je m'excuse j'essaie de comprendre ta technique de x+y > 1 mais je ne vois pas pourquoi inferieur a 1

J'ai pas hyper bien suivi la discussion, mais ça m'a l'air de venir du fait que l'équation de la droite (BC) est y=-x+1 . Donc M est dans ABC si et seulement si y<-x+1 , soit x+y<1 .

ElvadriaS, je reprends ton dernier post :

est un vecteur orthogonal à
Prenons par exemple
On a et
calculons . Maintenant calculons

Si est de même signe que ,
c'est à dire si le produit (-1)(x-1+y) est strictement positif
soit aussi si -x+1-y>0
ou encore Si x+y<1
alors M est dans le triangle ABC

rolands et toi avez l'air entièrement d'accord !

Re,
>> Rolands
pour ma part, j'utilise le logiciel SineQuaNon que j'ai découvert par le biais du forum de ce site. Pour insérer une image, tu clique sur l'icone image en bas de ton texte et tu inseres l'image (Cf. F.A.Q.)

>> ElvadriaS
tu as la méthode du Produit Scalaire aparement. Je te détailles quand même celle de Rolands :
Soit , on trace la droite parallele à BC passant par M. Elle coupe BC en M'.
Equation de (MM')
y=-x+p (car parallele à (BC):y=-x+1)
De plus, (MM') passe par M donc ses coordonnées vérifient l'equation,
ainsi donc
Donc MM' a pour equation

Trouvons les coordonnées de M':

on a le systeme

on trouve
ainsi on a
Si AM'<AB alors M est dans ABC, sinon il est dans l'autre triangle.
tu me suis ? (sauf erreurs)
Tomm-Bou