Inscription / Connexion Nouveau Sujet
Section d'un cube
Bonjour j'ai un exercice de géométrie dans l'espace que je n'arrive pas à faire. pouvez- vous m'aidez svp?
Il s'agit de construire un plan dans un cube, à parti des point M,P et N. J'ai commencé la construction et je sais comment la finir.
Mais le problème est que je n'arrive pas à prouver que les droites (P'd) et (PM) sont sécantes en un point I.
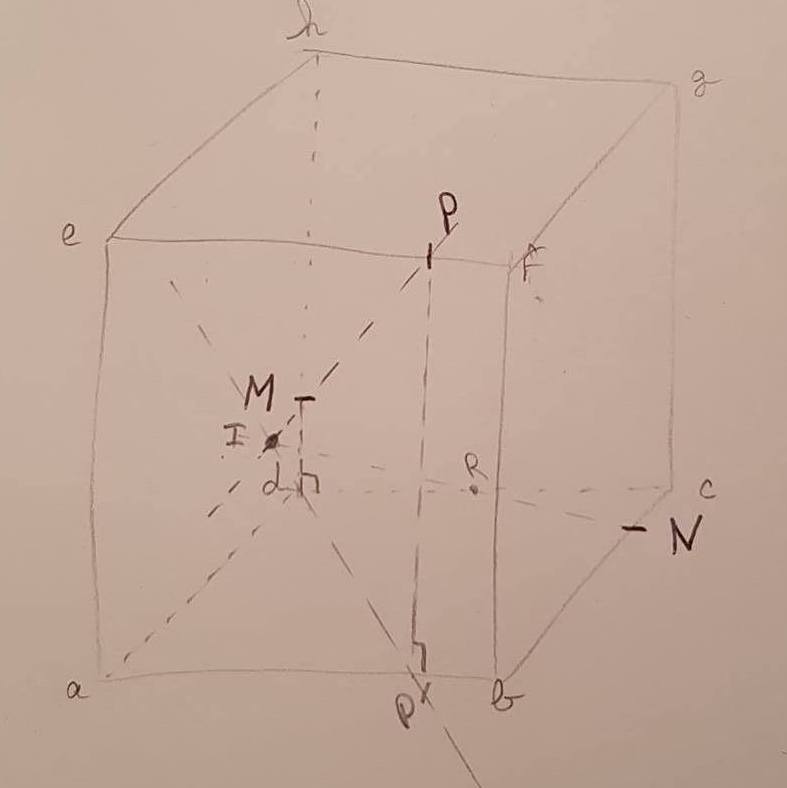
Voici la figure ci contre.
Merci d'avance pour votre aide.
Mais j'ai déjà dit que (pp') et (Md) sont parallèles car elles sont toutes les deux perpendiculaires à la même face adcb. Mais je ne vois pas quoi dire après ça. Pouvez-vous m'aider svp?
Mais je ne comprends pas comment ces deux droites peuvent être dans le même plan. Est-ce le plan MPP'D ?
Bien sûr, le plan PP'd contient (PP') qui est perallèle avec (dM).
Un droite qui a un point d dans un plan et qui est parallèle à une droite de ce plan est entièrement dans ce plan.
D'accord merci, donc (PM) et (dP') appartiennent au plan PP'd,
comme elles appartiennent au même plan alors elles sont coplanaires.
Si (PM) // (P'd) alors le segment md= PP' car (Md) et (PP4) sont parallèles entre elles et perpendiculaires à la face du dessous. Or Md n'est pas égale à PP4 donc (PM) n'est pas // à (P'd) et vu que c'est deux droites sont coplanaires, alors elles sont sécantes.
Est-ce bon?