Inscription / Connexion Nouveau Sujet
Section d'un cube par un plan.
Bonjour,
j'ai un exercice sur la géométrie dans l'espace :
ABCDEFGH est un cube. La droite (d) fait partie du plan (ADE). M est un point de la droite (DC). Construire la section du cube par le plan contenant la droite (d) et le point M.
Comme vous pouvez le voir sur la photo, j'ai tracé une parallèle à (d) passant par M et j'ai prolongé (d), (AD) et (ED) pour avoir des points d'intersection, mais je ne vois pas vraiment comment continuer.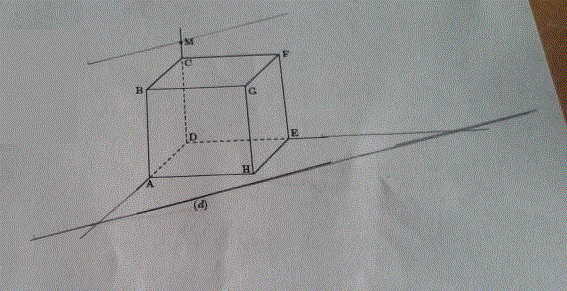
Bonjour,
Tu as presque terminé 
Donne des noms à tes points d'intersection ; P et Q ?
Les points M et P sont dans un même plan d'une face du cube.
Idem pour M et P .
Bonjour, oui d'accord, j'ai relié M et P ainsi que M et Q, de plus j'ai prolongé (AH) et (HE) pour avoir deux autres points d'intersection avec (d), ce qui m'a permis de faire la trace aussi sur les faces BGHA et HEFG.
Merci pour votre aide.
" pour avoir les deux autres points d'intersection avec (d) : intersection avec quoi ? Pas avec le plan (d; M) !
Certes, mais ensuite je peux relier ces nouveaux points d'intersection avec l'intersection de (MP) et (BA) ainsi que l'intersection de (FE) et (MQ).
Bonjour,
Il sa pourrait que le plan défini par M et (d) NE COUPE PAS le cube.
Comment le déterminer ?
Car ce peut être une aide décisive pour trouver l'intersection complète plan-cube !
J'avoue que j'ai du mal à comprendre votre remarque puisque l'on me demande justement de tracer la coupe du cube par le plan.
Bonjour,
Trost maitrise bien les intersections pour mener ce problème à terme.
Je propose cependant une démarche un peu différente.
J'ai repris la même position M et (d) que dans l'énoncé mais le cube est repéré ABCDEFGH de la manière habituelle
avec la face ABCD en position inférieure et EFGH respectivement au-dessus de ABCD.
Le premier point déterminé est l'intersection I de (d) et (DB) car si la droite (MI) intersecte le coté [BF] en J, le plan(M,(d)) intersecte le cube.
Soit alors K intersection de (MJ) avec [HF] : Une parallèle à (d) menée par K donne les intersections R et S sur les cotés de la face supérieure. On voit de suite si la section cherchée va être un triangle, un quadrilatère ou un pentagone.
sur la figure S est joint directement à J sur la face BCGF, tandis que R doit être joint à l'intersection L de (MR)avec le coté [AE], L étant joint à J pour terminer la section du cube.
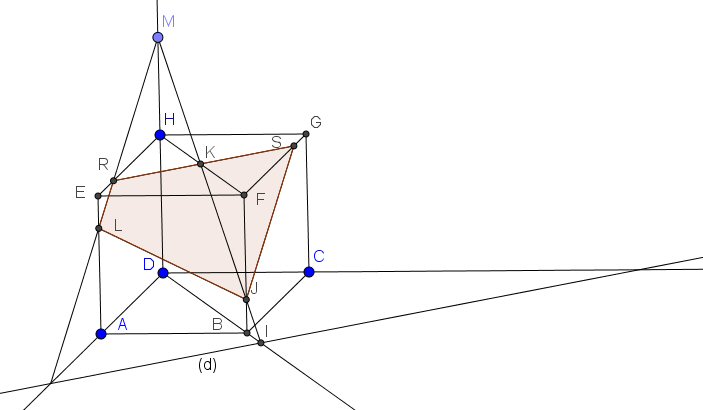
Si on écarte (d) dans le plan ABCD ci-dessus, on voit bien que MI peut couper la droite (BF)en dehors du segment [BF], il n'y a alors pas de section du cube par le plan (M,(d))
Joli et pas mal l'utilisation du plan BDHF 
On a tendance à ne vouloir utiliser que des plans des faces du cube. Pas toujours le plus simple !


